Unsupervised Community Detection with a Potts Model Hamiltonian, an Efficient Algorithmic Solution, and Applications in Digital Pathology
Paper and Code
Feb 05, 2020
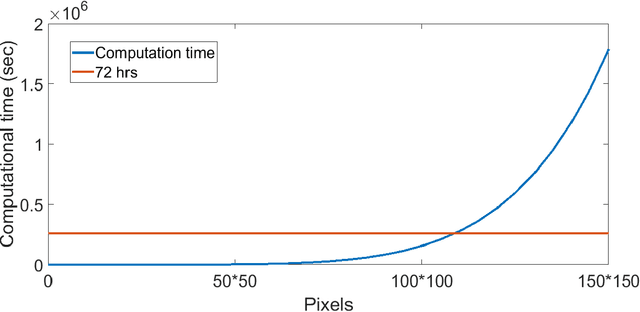
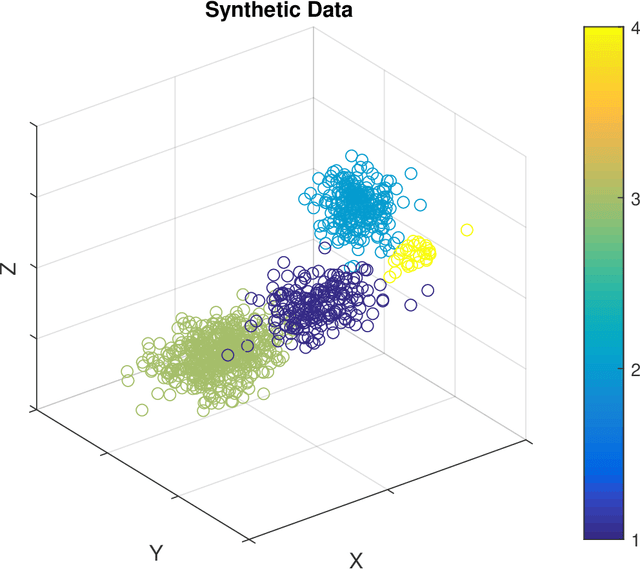
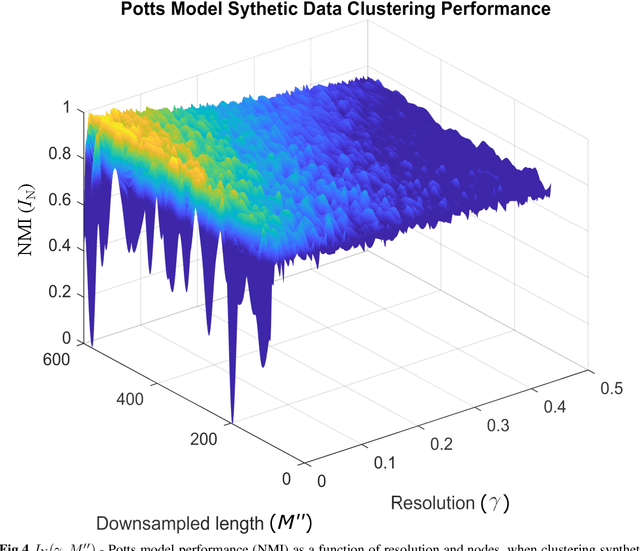
Unsupervised segmentation of large images using a Potts model Hamiltonian is unique in that segmentation is governed by a resolution parameter which scales the sensitivity to small clusters. Here, the input image is first modeled as a graph, which is then segmented by minimizing a Hamiltonian cost function defined on the graph and the respective segments. However, there exists no closed form solution of this optimization, and using previous iterative algorithmic solution techniques, the problem scales quadratically in the Input Length. Therefore, while Potts model segmentation gives accurate segmentation, it is grossly underutilized as an unsupervised learning technique. We propose a fast statistical down-sampling of input image pixels based on the respective color features, and a new iterative method to minimize the Potts model energy considering pixel to segment relationship. This method is generalizable and can be extended for image pixel texture features as well as spatial features. We demonstrate that this new method is highly efficient, and outperforms existing methods for Potts model based image segmentation. We demonstrate the application of our method in medical microscopy image segmentation; particularly, in segmenting renal glomerular micro-environment in renal pathology. Our method is not limited to image segmentation, and can be extended to any image/data segmentation/clustering task for arbitrary datasets with discrete features.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge