Inference of hidden structures in complex physical systems by multi-scale clustering

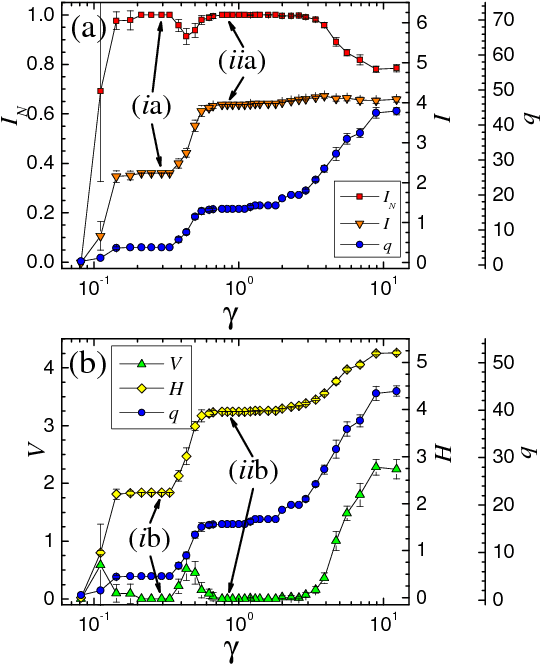
We survey the application of a relatively new branch of statistical physics--"community detection"-- to data mining. In particular, we focus on the diagnosis of materials and automated image segmentation. Community detection describes the quest of partitioning a complex system involving many elements into optimally decoupled subsets or communities of such elements. We review a multiresolution variant which is used to ascertain structures at different spatial and temporal scales. Significant patterns are obtained by examining the correlations between different independent solvers. Similar to other combinatorial optimization problems in the NP complexity class, community detection exhibits several phases. Typically, illuminating orders are revealed by choosing parameters that lead to extremal information theory correlations.

Automatic Segmentation of Fluorescence Lifetime Microscopy Images of Cells Using Multi-Resolution Community Detection

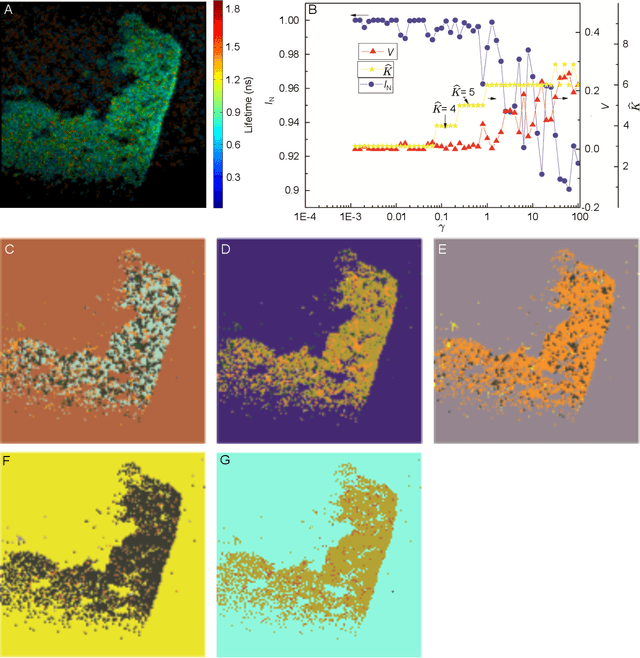
We have developed an automatic method for segmenting fluorescence lifetime (FLT) imaging microscopy (FLIM) images of cells inspired by a multi-resolution community detection (MCD) based network segmentation method. The image processing problem is framed as identifying segments with respective average FLTs against a background in FLIM images. The proposed method segments a FLIM image for a given resolution of the network composed using image pixels as the nodes and similarity between the pixels as the edges. In the resulting segmentation, low network resolution leads to larger segments and high network resolution leads to smaller segments. Further, the mean-square error (MSE) in estimating the FLT segments in a FLIM image using the proposed method was found to be consistently decreasing with increasing resolution of the corresponding network. The proposed MCD method outperformed a popular spectral clustering based method in performing FLIM image segmentation. The spectral segmentation method introduced noisy segments in its output at high resolution. It was unable to offer a consistent decrease in MSE with increasing resolution.

A Replica Inference Approach to Unsupervised Multi-Scale Image Segmentation

We apply a replica inference based Potts model method to unsupervised image segmentation on multiple scales. This approach was inspired by the statistical mechanics problem of "community detection" and its phase diagram. Specifically, the problem is cast as identifying tightly bound clusters ("communities" or "solutes") against a background or "solvent". Within our multiresolution approach, we compute information theory based correlations among multiple solutions ("replicas") of the same graph over a range of resolutions. Significant multiresolution structures are identified by replica correlations as manifest in information theory overlaps. With the aid of these correlations as well as thermodynamic measures, the phase diagram of the corresponding Potts model is analyzed both at zero and finite temperatures. Optimal parameters corresponding to a sensible unsupervised segmentation correspond to the "easy phase" of the Potts model. Our algorithm is fast and shown to be at least as accurate as the best algorithms to date and to be especially suited to the detection of camouflaged images.