Inference of hidden structures in complex physical systems by multi-scale clustering
Paper and Code
Jan 14, 2016
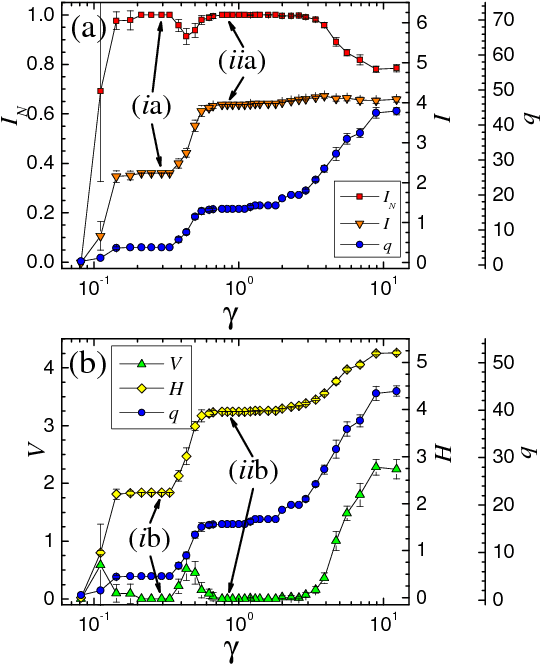

We survey the application of a relatively new branch of statistical physics--"community detection"-- to data mining. In particular, we focus on the diagnosis of materials and automated image segmentation. Community detection describes the quest of partitioning a complex system involving many elements into optimally decoupled subsets or communities of such elements. We review a multiresolution variant which is used to ascertain structures at different spatial and temporal scales. Significant patterns are obtained by examining the correlations between different independent solvers. Similar to other combinatorial optimization problems in the NP complexity class, community detection exhibits several phases. Typically, illuminating orders are revealed by choosing parameters that lead to extremal information theory correlations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge