Multi-Class classification of vulnerabilities in Smart Contracts using AWD-LSTM, with pre-trained encoder inspired from natural language processing

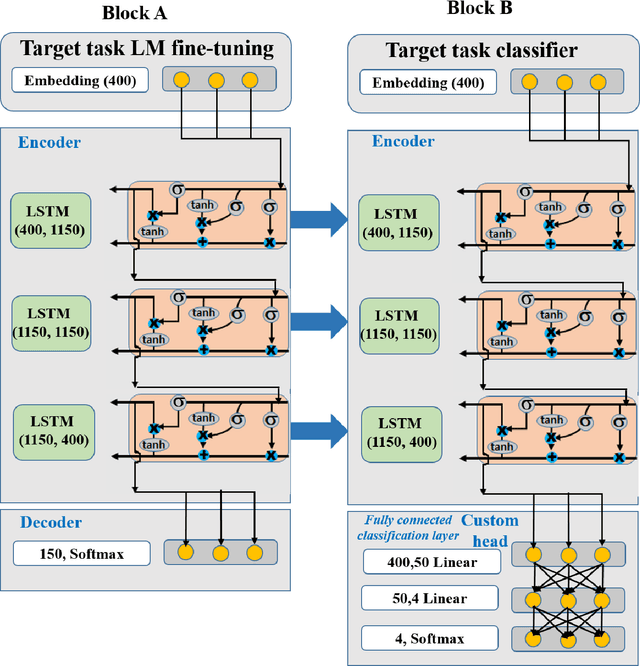
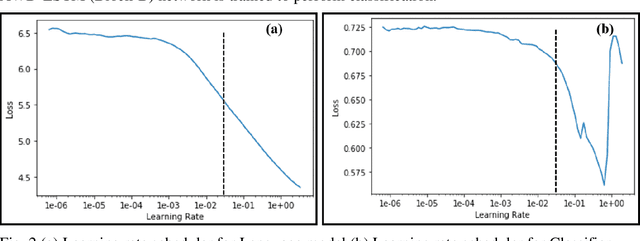
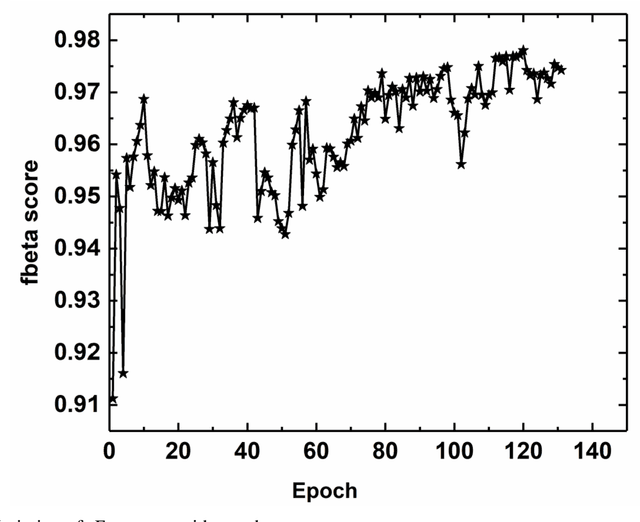
Vulnerability detection and safety of smart contracts are of paramount importance because of their immutable nature. Symbolic tools like OYENTE and MAIAN are typically used for vulnerability prediction in smart contracts. As these tools are computationally expensive, they are typically used to detect vulnerabilities until some predefined invocation depth. These tools require more search time as the invocation depth increases. Since the number of smart contracts is increasing exponentially, it is difficult to analyze the contracts using these traditional tools. Recently a machine learning technique called Long Short Term Memory (LSTM) has been used for binary classification, i.e., to predict whether a smart contract is vulnerable or not. This technique requires nearly constant search time as the invocation depth increases. In the present article, we have shown a multi-class classification, where we classify a smart contract in Suicidal, Prodigal, Greedy, or Normal categories. We used Average Stochastic Gradient Descent Weight-Dropped LSTM (AWD-LSTM), which is a variant of LSTM, to perform classification. We reduced the class imbalance (a large number of normal contracts as compared to other categories) by considering only the distinct opcode combination for normal contracts. We have achieved a weighted average Fbeta score of 90.0%. Hence, such techniques can be used to analyze a large number of smart contracts and help to improve the security of these contracts.

Visual Machine Learning: Insight through Eigenvectors, Chladni patterns and community detection in 2D particulate structures

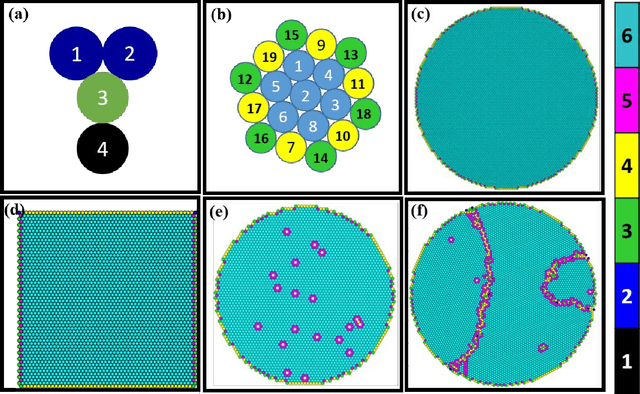
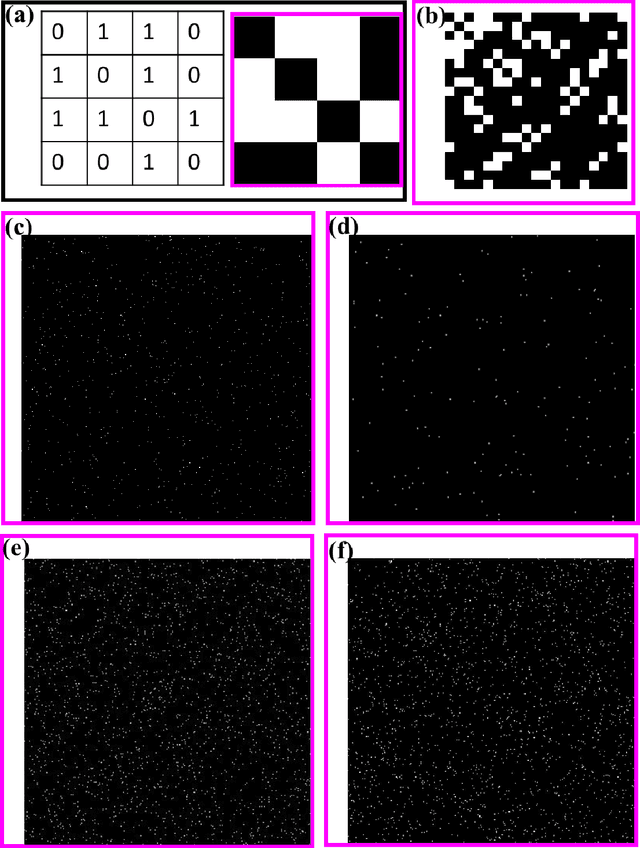
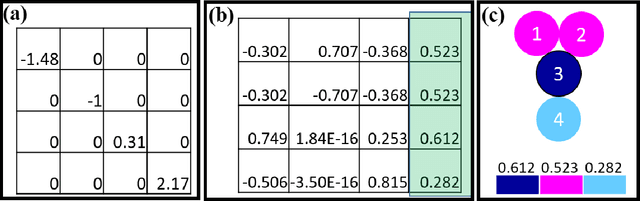
Machine learning (ML) is quickly emerging as a powerful tool with diverse applications across an extremely broad spectrum of disciplines and commercial endeavors. Typically, ML is used as a black box that provides little illuminating rationalization of its output. In the current work, we aim to better understand the generic intuition underlying unsupervised ML with a focus on physical systems. The systems that are studied here as test cases comprise of six different 2-dimensional (2-D) particulate systems of different complexities. It is noted that the findings of this study are generic to any unsupervised ML problem and are not restricted to materials systems alone. Three rudimentary unsupervised ML techniques are employed on the adjacency (connectivity) matrix of the six studied systems: (i) using principal eigenvalue and eigenvectors of the adjacency matrix, (ii) spectral decomposition, and (iii) a Potts model based community detection technique in which a modularity function is maximized. We demonstrate that, while solving a completely classical problem, ML technique produces features that are distinctly connected to quantum mechanical solutions. Dissecting these features help us to understand the deep connection between the classical non-linear world and the quantum mechanical linear world through the kaleidoscope of ML technique, which might have far reaching consequences both in the arena of physical sciences and ML.