A new nature inspired modularity function adapted for unsupervised learning involving spatially embedded networks: A comparative analysis

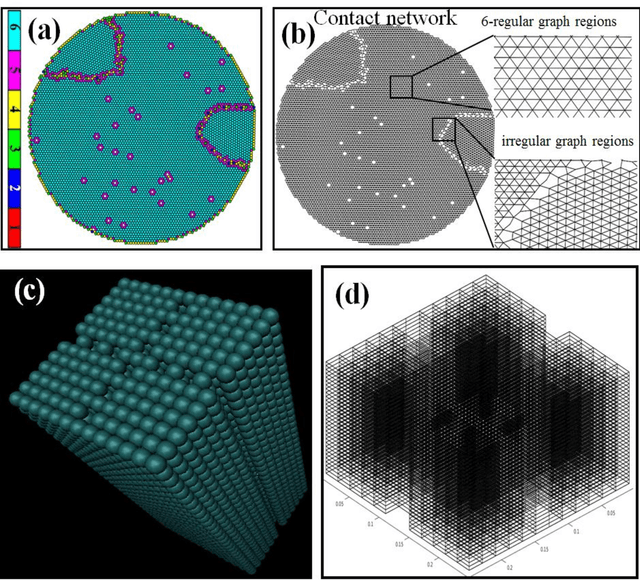
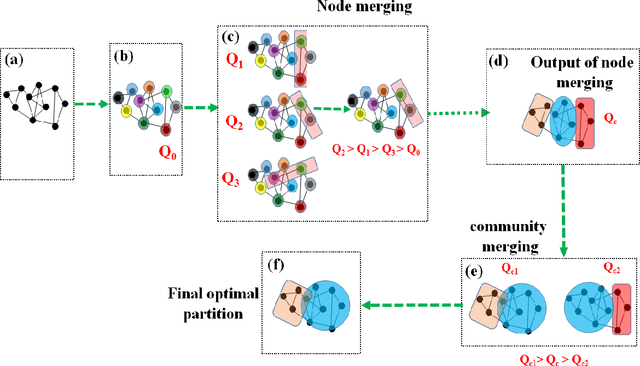
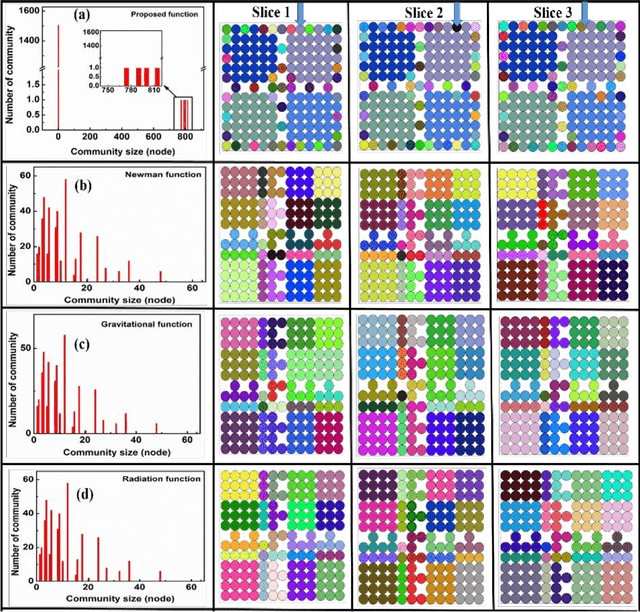
Unsupervised machine learning methods can be of great help in many traditional engineering disciplines, where huge amount of labeled data is not readily available or is extremely difficult or costly to generate. Two specific examples include the structure of granular materials and atomic structure of metallic glasses. While the former is critically important for several hundreds of billion dollars global industries, the latter is still a big puzzle in fundamental science. One thing is common in both the examples is that the particles are the elements of the ensembles that are embedded in Euclidean space and one can create a spatially embedded network to represent their key features. Some recent studies show that clustering, which generically refers to unsupervised learning, holds great promise in partitioning these networks. In many complex networks, the spatial information of nodes play very important role in determining the network properties. So understanding the structure of such networks is very crucial. We have compared the performance of our newly developed modularity function with some of the well-known modularity functions. We performed this comparison by finding the best partition in 2D and 3D granular assemblies. We show that for the class of networks considered in this article, our method produce much better results than the competing methods.

Visual Machine Learning: Insight through Eigenvectors, Chladni patterns and community detection in 2D particulate structures

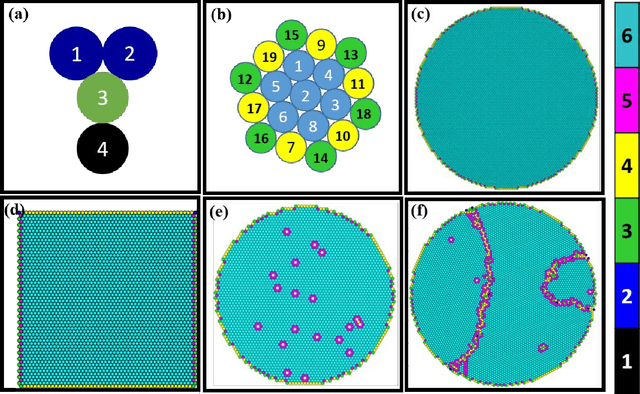
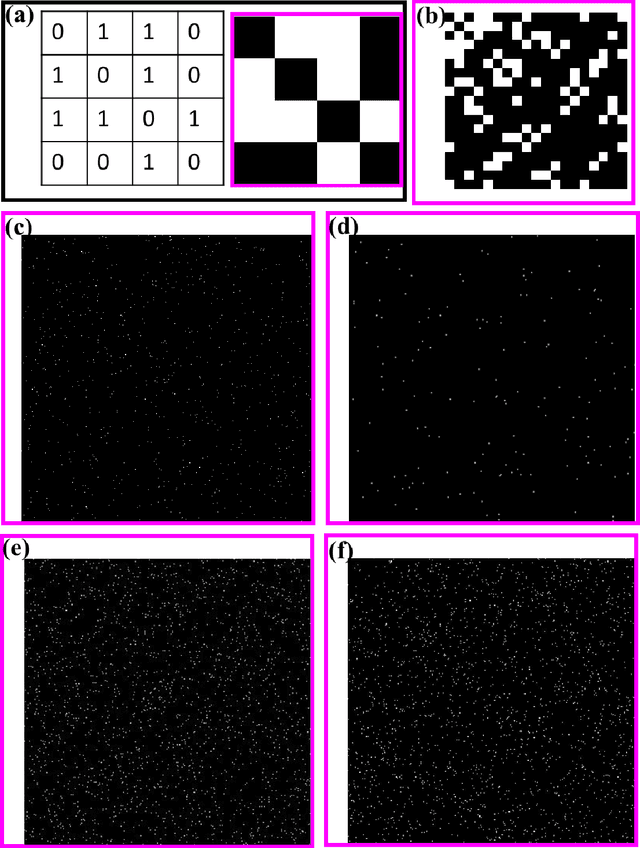
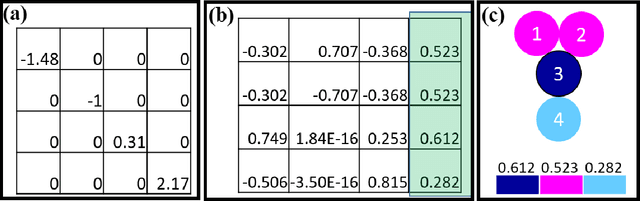
Machine learning (ML) is quickly emerging as a powerful tool with diverse applications across an extremely broad spectrum of disciplines and commercial endeavors. Typically, ML is used as a black box that provides little illuminating rationalization of its output. In the current work, we aim to better understand the generic intuition underlying unsupervised ML with a focus on physical systems. The systems that are studied here as test cases comprise of six different 2-dimensional (2-D) particulate systems of different complexities. It is noted that the findings of this study are generic to any unsupervised ML problem and are not restricted to materials systems alone. Three rudimentary unsupervised ML techniques are employed on the adjacency (connectivity) matrix of the six studied systems: (i) using principal eigenvalue and eigenvectors of the adjacency matrix, (ii) spectral decomposition, and (iii) a Potts model based community detection technique in which a modularity function is maximized. We demonstrate that, while solving a completely classical problem, ML technique produces features that are distinctly connected to quantum mechanical solutions. Dissecting these features help us to understand the deep connection between the classical non-linear world and the quantum mechanical linear world through the kaleidoscope of ML technique, which might have far reaching consequences both in the arena of physical sciences and ML.