Integral regularization PINNs for evolution equations

Evolution equations, including both ordinary differential equations (ODEs) and partial differential equations (PDEs), play a pivotal role in modeling dynamic systems. However, achieving accurate long-time integration for these equations remains a significant challenge. While physics-informed neural networks (PINNs) provide a mesh-free framework for solving PDEs, they often suffer from temporal error accumulation, which limits their effectiveness in capturing long-time behaviors. To alleviate this issue, we propose integral regularization PINNs (IR-PINNs), a novel approach that enhances temporal accuracy by incorporating an integral-based residual term into the loss function. This method divides the entire time interval into smaller sub-intervals and enforces constraints over these sub-intervals, thereby improving the resolution and correlation of temporal dynamics. Furthermore, IR-PINNs leverage adaptive sampling to dynamically refine the distribution of collocation points based on the evolving solution, ensuring higher accuracy in regions with sharp gradients or rapid variations. Numerical experiments on benchmark problems demonstrate that IR-PINNs outperform original PINNs and other state-of-the-art methods in capturing long-time behaviors, offering a robust and accurate solution for evolution equations.

A hybrid FEM-PINN method for time-dependent partial differential equations

In this work, we present a hybrid numerical method for solving evolution partial differential equations (PDEs) by merging the time finite element method with deep neural networks. In contrast to the conventional deep learning-based formulation where the neural network is defined on a spatiotemporal domain, our methodology utilizes finite element basis functions in the time direction where the space-dependent coefficients are defined as the output of a neural network. We then apply the Galerkin or collocation projection in the time direction to obtain a system of PDEs for the space-dependent coefficients which is approximated in the framework of PINN. The advantages of such a hybrid formulation are twofold: statistical errors are avoided for the integral in the time direction, and the neural network's output can be regarded as a set of reduced spatial basis functions. To further alleviate the difficulties from high dimensionality and low regularity, we have developed an adaptive sampling strategy that refines the training set. More specifically, we use an explicit density model to approximate the distribution induced by the PDE residual and then augment the training set with new time-dependent random samples given by the learned density model. The effectiveness and efficiency of our proposed method have been demonstrated through a series of numerical experiments.

MEL: Efficient Multi-Task Evolutionary Learning for High-Dimensional Feature Selection

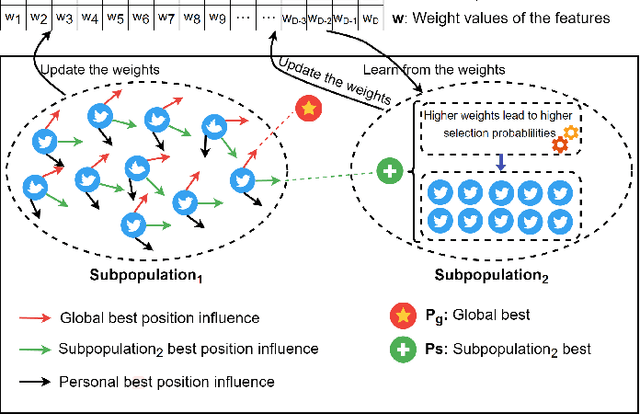
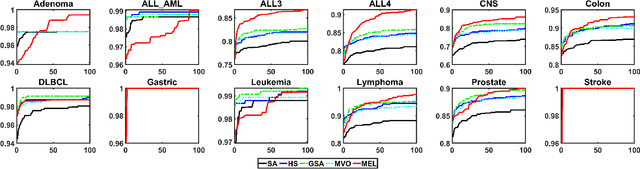
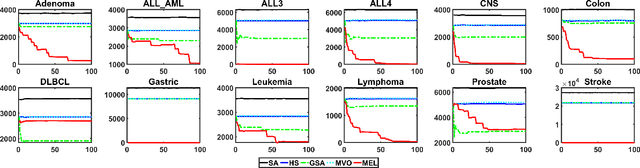
Feature selection is a crucial step in data mining to enhance model performance by reducing data dimensionality. However, the increasing dimensionality of collected data exacerbates the challenge known as the "curse of dimensionality", where computation grows exponentially with the number of dimensions. To tackle this issue, evolutionary computational (EC) approaches have gained popularity due to their simplicity and applicability. Unfortunately, the diverse designs of EC methods result in varying abilities to handle different data, often underutilizing and not sharing information effectively. In this paper, we propose a novel approach called PSO-based Multi-task Evolutionary Learning (MEL) that leverages multi-task learning to address these challenges. By incorporating information sharing between different feature selection tasks, MEL achieves enhanced learning ability and efficiency. We evaluate the effectiveness of MEL through extensive experiments on 22 high-dimensional datasets. Comparing against 24 EC approaches, our method exhibits strong competitiveness. Additionally, we have open-sourced our code on GitHub at https://github.com/wangxb96/MEL.