Bounded KRnet and its applications to density estimation and approximation
Paper and Code
May 15, 2023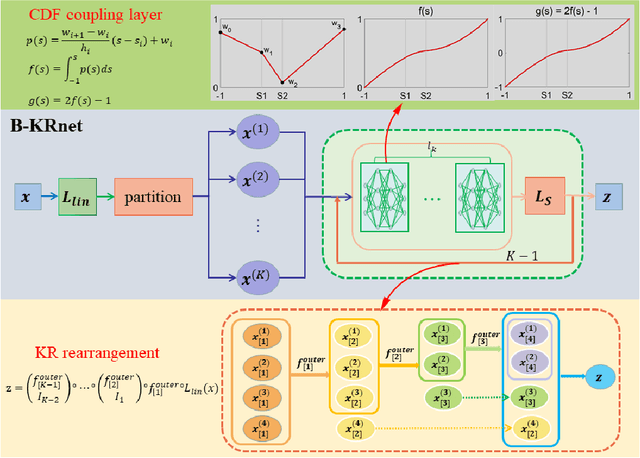
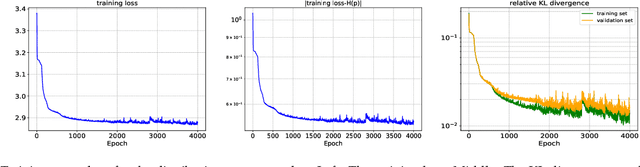
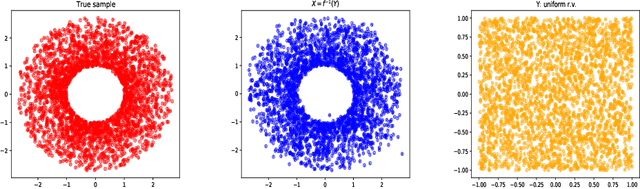
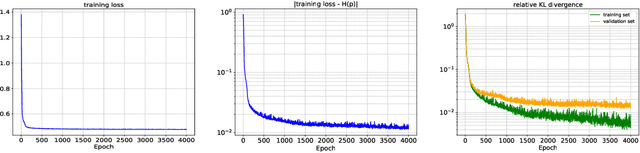
In this paper, we develop an invertible mapping, called B-KRnet, on a bounded domain and apply it to density estimation/approximation for data or the solutions of PDEs such as the Fokker-Planck equation and the Keller-Segel equation. Similar to KRnet, the structure of B-KRnet adapts the triangular form of the Knothe-Rosenblatt rearrangement into a normalizing flow model. The main difference between B-KRnet and KRnet is that B-KRnet is defined on a hypercube while KRnet is defined on the whole space, in other words, we introduce a new mechanism in B-KRnet to maintain the exact invertibility. Using B-KRnet as a transport map, we obtain an explicit probability density function (PDF) model that corresponds to the pushforward of a prior (uniform) distribution on the hypercube. To approximate PDFs defined on a bounded computational domain, B-KRnet is more effective than KRnet. By coupling KRnet and B-KRnet, we can also define a deep generative model on a high-dimensional domain where some dimensions are bounded and other dimensions are unbounded. A typical case is the solution of the stationary kinetic Fokker-Planck equation, which is a PDF of position and momentum. Based on B-KRnet, we develop an adaptive learning approach to approximate partial differential equations whose solutions are PDFs or can be regarded as a PDF. In addition, we apply B-KRnet to density estimation when only data are available. A variety of numerical experiments is presented to demonstrate the effectiveness of B-KRnet.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge