Dimension-reduced KRnet maps for high-dimensional Bayesian inverse problems

We present a dimension-reduced KRnet map approach (DR-KRnet) for high-dimensional Bayesian inverse problems, which is based on an explicit construction of a map that pushes forward the prior measure to the posterior measure in the latent space. Our approach consists of two main components: data-driven VAE prior and density approximation of the posterior of the latent variable. In reality, it may not be trivial to initialize a prior distribution that is consistent with available prior data; in other words, the complex prior information is often beyond simple hand-crafted priors. We employ variational autoencoder (VAE) to approximate the underlying distribution of the prior dataset, which is achieved through a latent variable and a decoder. Using the decoder provided by the VAE prior, we reformulate the problem in a low-dimensional latent space. In particular, we seek an invertible transport map given by KRnet to approximate the posterior distribution of the latent variable. Moreover, an efficient physics-constrained surrogate model without any labeled data is constructed to reduce the computational cost of solving both forward and adjoint problems involved in likelihood computation. With numerical experiments, we demonstrate the accuracy and efficiency of DR-KRnet for high-dimensional Bayesian inverse problems.

Streaming probabilistic tensor train decomposition

The Bayesian streaming tensor decomposition method is a novel method to discover the low-rank approximation of streaming data. However, when the streaming data comes from a high-order tensor, tensor structures of existing Bayesian streaming tensor decomposition algorithms may not be suitable in terms of representation and computation power. In this paper, we present a new Bayesian streaming tensor decomposition method based on tensor train (TT) decomposition. Especially, TT decomposition renders an efficient approach to represent high-order tensors. By exploiting the streaming variational inference (SVI) framework and TT decomposition, we can estimate the latent structure of high-order incomplete noisy streaming tensors. The experiments in synthetic and real-world data show the accuracy of our algorithm compared to the state-of-the-art Bayesian streaming tensor decomposition approaches.

Tensor Train Random Projection

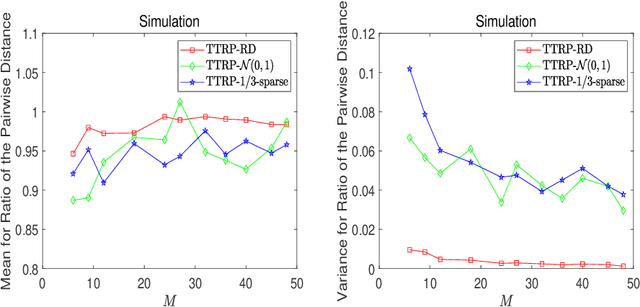
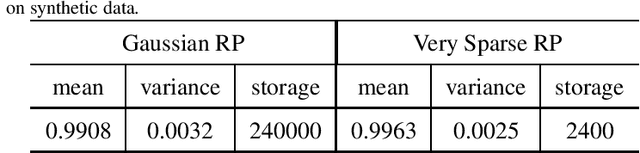
This work proposes a novel tensor train random projection (TTRP) method for dimension reduction, where the pairwise distances can be approximately preserved. Based on the tensor train format, this new random projection method can speed up the computation for high dimensional problems and requires less storage with little loss in accuracy, compared with existing methods (e.g., very sparse random projection). Our TTRP is systematically constructed through a rank-one TT-format with Rademacher random variables, which results in efficient projection with small variances. The isometry property of TTRP is proven in this work, and detailed numerical experiments with data sets (synthetic, MNIST and CIFAR-10) are conducted to demonstrate the efficiency of TTRP.