Fast Equivariant Imaging: Acceleration for Unsupervised Learning via Augmented Lagrangian and Auxiliary PnP Denoisers

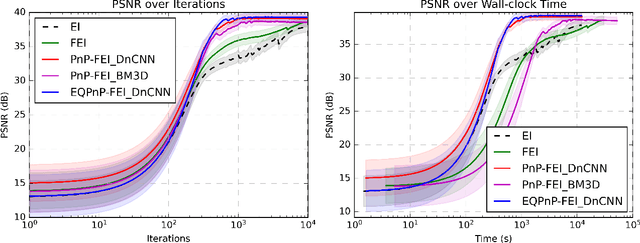
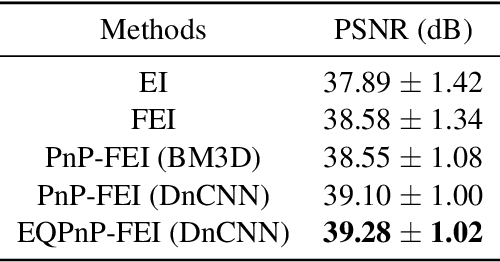
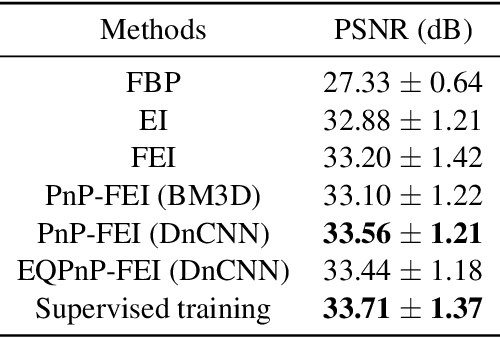
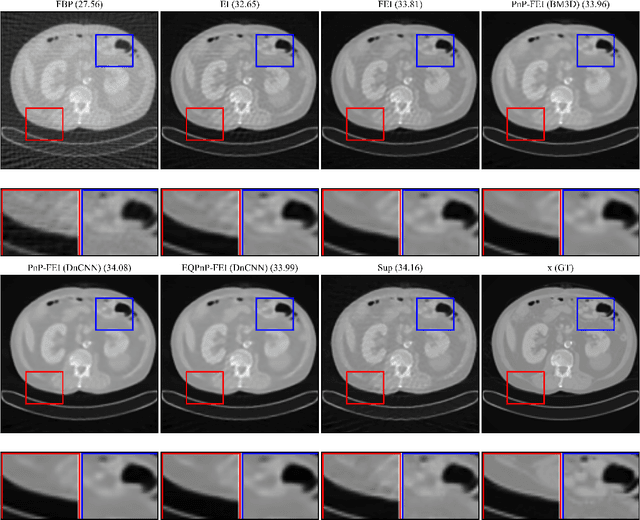
We propose Fast Equivariant Imaging (FEI), a novel unsupervised learning framework to efficiently train deep imaging networks without ground-truth data. From the perspective of reformulating the Equivariant Imaging based optimization problem via the method of Lagrange multipliers and utilizing plug-and-play denoisers, this novel unsupervised scheme shows superior efficiency and performance compared to vanilla Equivariant Imaging paradigm. In particular, our PnP-FEI scheme achieves an order-of-magnitude (10x) acceleration over standard EI on training U-Net with CT100 dataset for X-ray CT reconstruction, with improved generalization performance.

Sketched Equivariant Imaging Regularization and Deep Internal Learning for Inverse Problems

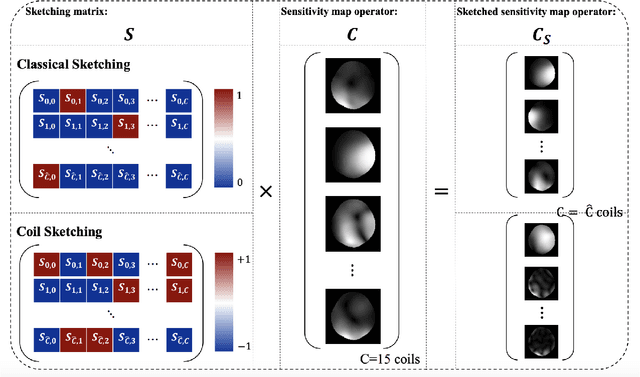
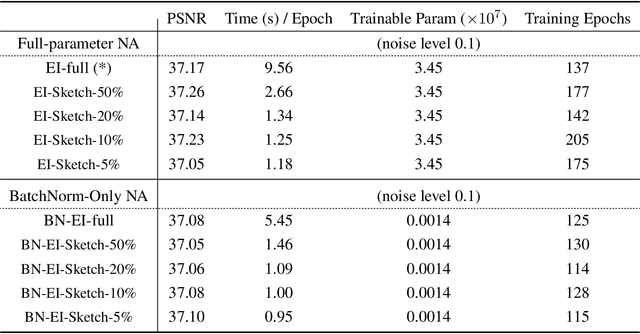
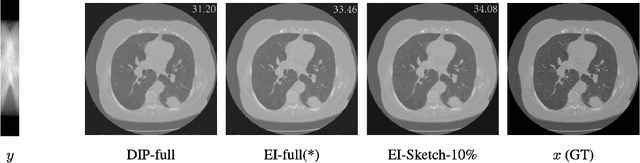
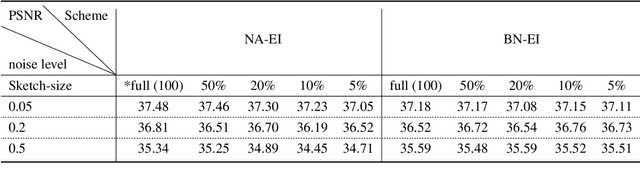
Equivariant Imaging (EI) regularization has become the de-facto technique for unsupervised training of deep imaging networks, without any need of ground-truth data. Observing that the EI-based unsupervised training paradigm currently has significant computational redundancy leading to inefficiency in high-dimensional applications, we propose a sketched EI regularization which leverages the randomized sketching techniques for acceleration. We then extend our sketched EI regularization to develop an accelerated deep internal learning framework -- Sketched Equivariant Deep Image Prior (Sk.EI-DIP), which can be efficiently applied for single-image and task-adapted reconstruction. Our numerical study on X-ray CT image reconstruction tasks demonstrate that our approach can achieve order-of-magnitude computational acceleration over standard EI-based counterpart in single-input setting, and network adaptation at test time.

A Comparative Study of Variational Autoencoders, Normalizing Flows, and Score-based Diffusion Models for Electrical Impedance Tomography

Electrical Impedance Tomography (EIT) is a widely employed imaging technique in industrial inspection, geophysical prospecting, and medical imaging. However, the inherent nonlinearity and ill-posedness of EIT image reconstruction present challenges for classical regularization techniques, such as the critical selection of regularization terms and the lack of prior knowledge. Deep generative models (DGMs) have been shown to play a crucial role in learning implicit regularizers and prior knowledge. This study aims to investigate the potential of three DGMs-variational autoencoder networks, normalizing flow, and score-based diffusion model-to learn implicit regularizers in learning-based EIT imaging. We first introduce background information on EIT imaging and its inverse problem formulation. Next, we propose three algorithms for performing EIT inverse problems based on corresponding DGMs. Finally, we present numerical and visual experiments, which reveal that (1) no single method consistently outperforms the others across all settings, and (2) when reconstructing an object with 2 anomalies using a well-trained model based on a training dataset containing 4 anomalies, the conditional normalizing flow model (CNF) exhibits the best generalization in low-level noise, while the conditional score-based diffusion model (CSD*) demonstrates the best generalization in high-level noise settings. We hope our preliminary efforts will encourage other researchers to assess their DGMs in EIT and other nonlinear inverse problems.

Enhancing Electrical Impedance Tomography reconstruction using Learned Half-Quadratic Splitting Networks with Anderson Acceleration

Electrical Impedance Tomography (EIT) is widely applied in medical diagnosis, industrial inspection, and environmental monitoring. Combining the physical principles of the imaging system with the advantages of data-driven deep learning networks, physics-embedded deep unrolling networks have recently emerged as a promising solution in computational imaging. However, the inherent nonlinear and ill-posed properties of EIT image reconstruction still present challenges to existing methods in terms of accuracy and stability. To tackle this challenge, we propose the learned half-quadratic splitting (HQSNet) algorithm for incorporating physics into learning-based EIT imaging. We then apply Anderson acceleration (AA) to the HQSNet algorithm, denoted as AA-HQSNet, which can be interpreted as AA applied to the Gauss-Newton step and the learned proximal gradient descent step of the HQSNet, respectively. AA is a widely-used technique for accelerating the convergence of fixed-point iterative algorithms and has gained significant interest in numerical optimization and machine learning. However, the technique has received little attention in the inverse problems community thus far. Employing AA enhances the convergence rate compared to the standard HQSNet while simultaneously avoiding artifacts in the reconstructions. Lastly, we conduct rigorous numerical and visual experiments to show that the AA module strengthens the HQSNet, leading to robust, accurate, and considerably superior reconstructions compared to state-of-the-art methods. Our Anderson acceleration scheme to enhance HQSNet is generic and can be applied to improve the performance of various physics-embedded deep learning methods.