On Estimating the Gradient of the Expected Information Gain in Bayesian Experimental Design

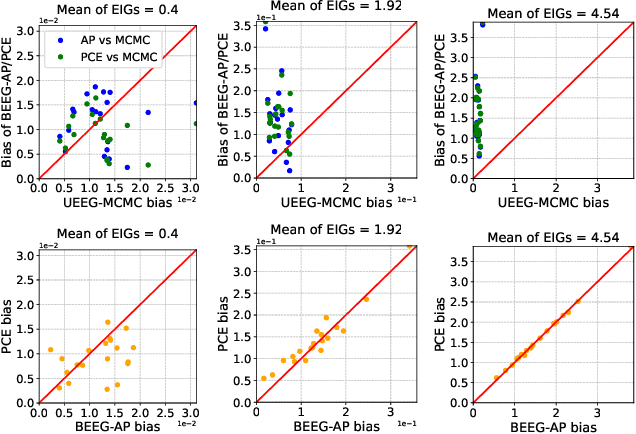
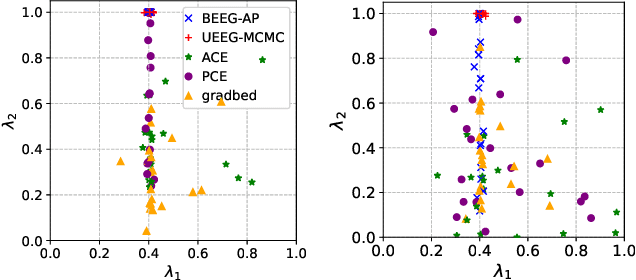
Bayesian Experimental Design (BED), which aims to find the optimal experimental conditions for Bayesian inference, is usually posed as to optimize the expected information gain (EIG). The gradient information is often needed for efficient EIG optimization, and as a result the ability to estimate the gradient of EIG is essential for BED problems. The primary goal of this work is to develop methods for estimating the gradient of EIG, which, combined with the stochastic gradient descent algorithms, result in efficient optimization of EIG. Specifically, we first introduce a posterior expected representation of the EIG gradient with respect to the design variables. Based on this, we propose two methods for estimating the EIG gradient, UEEG-MCMC that leverages posterior samples generated through Markov Chain Monte Carlo (MCMC) to estimate the EIG gradient, and BEEG-AP that focuses on achieving high simulation efficiency by repeatedly using parameter samples. Theoretical analysis and numerical studies illustrate that UEEG-MCMC is robust agains the actual EIG value, while BEEG-AP is more efficient when the EIG value to be optimized is small. Moreover, both methods show superior performance compared to several popular benchmarks in our numerical experiments.

An approximate {KLD} based experimental design for models with intractable likelihoods

Data collection is a critical step in statistical inference and data science, and the goal of statistical experimental design (ED) is to find the data collection setup that can provide most information for the inference. In this work we consider a special type of ED problems where the likelihoods are not available in a closed form. In this case, the popular information-theoretic Kullback-Leibler divergence (KLD) based design criterion can not be used directly, as it requires to evaluate the likelihood function. To address the issue, we derive a new utility function, which is a lower bound of the original KLD utility. This lower bound is expressed in terms of the summation of two or more entropies in the data space, and thus can be evaluated efficiently via entropy estimation methods. We provide several numerical examples to demonstrate the performance of the proposed method.