Model-based reconstructions for quantitative imaging in photoacoustic tomography

The reconstruction task in photoacoustic tomography can vary a lot depending on measured targets, geometry, and especially the quantity we want to recover. Specifically, as the signal is generated due to the coupling of light and sound by the photoacoustic effect, we have the possibility to recover acoustic as well as optical tissue parameters. This is referred to as quantitative imaging, i.e, correct recovery of physical parameters and not just a qualitative image. In this chapter, we aim to give an overview on established reconstruction techniques in photoacoustic tomography. We start with modelling of the optical and acoustic phenomena, necessary for a reliable recovery of quantitative values. Furthermore, we give an overview of approaches for the tomographic reconstruction problem with an emphasis on the recovery of quantitative values, from direct and fast analytic approaches to computationally involved optimisation based techniques and recent data-driven approaches.

Utilizing variational autoencoders in the Bayesian inverse problem of photoacoustic tomography

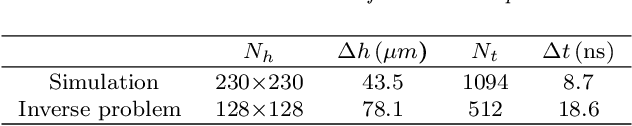
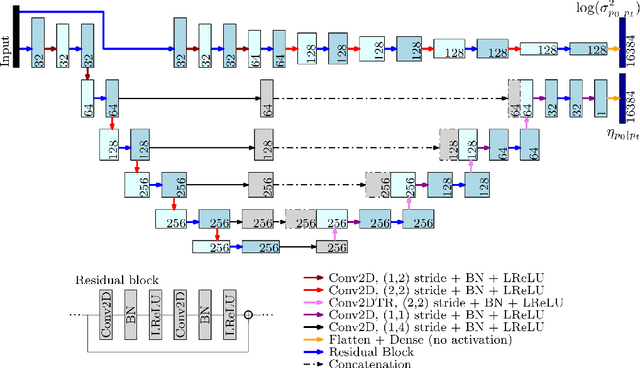
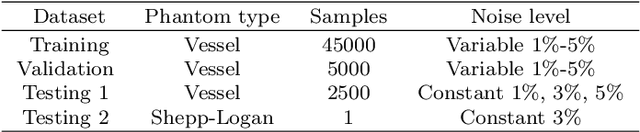
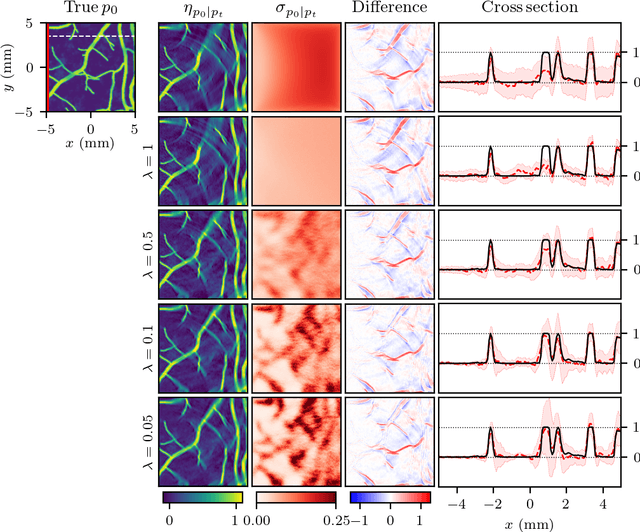
There has been an increasing interest in utilizing machine learning methods in inverse problems and imaging. Most of the work has, however, concentrated on image reconstruction problems, and the number of studies regarding the full solution of the inverse problem is limited. In this work, we study a machine learning based approach for the Bayesian inverse problem of photoacoustic tomography. We develop an approach for estimating the posterior distribution in photoacoustic tomography using an approach based on the variational autoencoder. The approach is evaluated with numerical simulations and compared to the solution of the inverse problem using a Bayesian approach.

On Learned Operator Correction

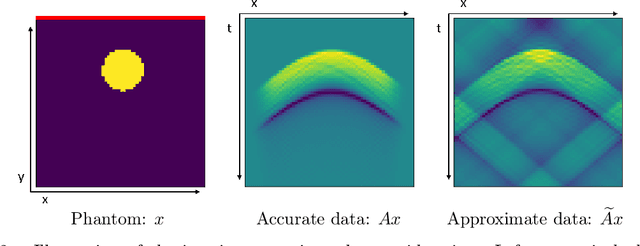
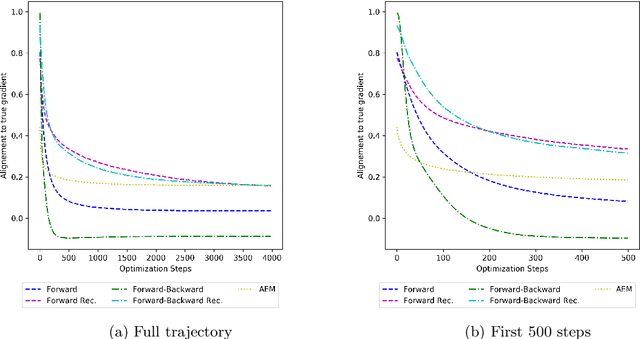
We discuss the possibility to learn a data-driven explicit model correction for inverse problems and whether such a model correction can be used within a variational framework to obtain regularised reconstructions. This paper discusses the conceptual difficulty to learn such a forward model correction and proceeds to present a possible solution as forward-backward correction that explicitly corrects in both data and solution spaces. We then derive conditions under which solutions to the variational problem with a learned correction converge to solutions obtained with the correct operator. The proposed approach is evaluated on an application to limited view photoacoustic tomography and compared to the established framework of Bayesian approximation error method.