On Learned Operator Correction

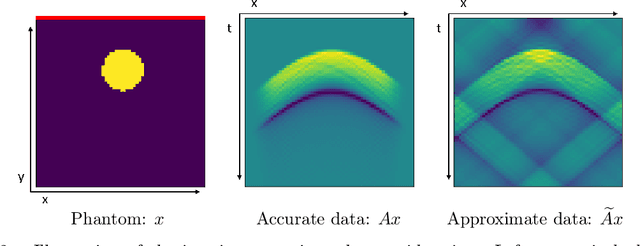
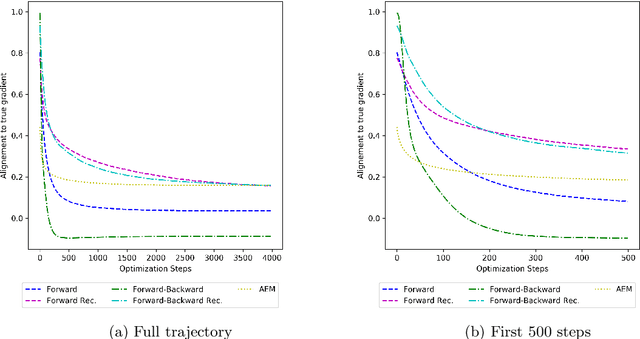
We discuss the possibility to learn a data-driven explicit model correction for inverse problems and whether such a model correction can be used within a variational framework to obtain regularised reconstructions. This paper discusses the conceptual difficulty to learn such a forward model correction and proceeds to present a possible solution as forward-backward correction that explicitly corrects in both data and solution spaces. We then derive conditions under which solutions to the variational problem with a learned correction converge to solutions obtained with the correct operator. The proposed approach is evaluated on an application to limited view photoacoustic tomography and compared to the established framework of Bayesian approximation error method.