Sebastian Lunz
Learned convex regularizers for inverse problems
Aug 06, 2020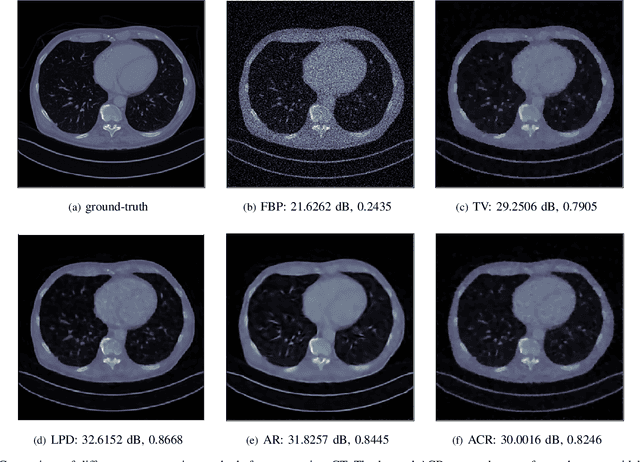

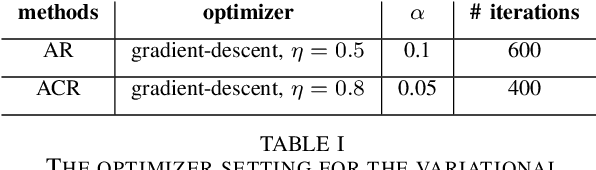
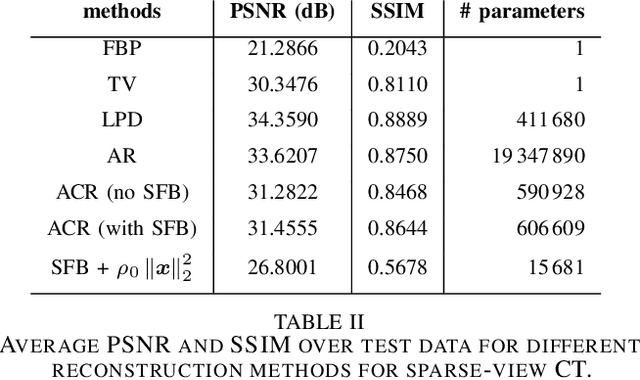
Abstract:We consider the variational reconstruction framework for inverse problems and propose to learn a data-adaptive input-convex neural network (ICNN) as the regularization functional. The ICNN-based convex regularizer is trained adversarially to discern ground-truth images from unregularized reconstructions. Convexity of the regularizer is attractive since (i) one can establish analytical convergence guarantees for the corresponding variational reconstruction problem and (ii) devise efficient and provable algorithms for reconstruction. In particular, we show that the optimal solution to the variational problem converges to the ground-truth if the penalty parameter decays sub-linearly with respect to the norm of the noise. Further, we prove the existence of a subgradient-based algorithm that leads to monotonically decreasing error in the parameter space with iterations. To demonstrate the performance of our approach for solving inverse problems, we consider the tasks of deblurring natural images and reconstructing images in computed tomography (CT), and show that the proposed convex regularizer is at least competitive with and sometimes superior to state-of-the-art data-driven techniques for inverse problems.
On Learned Operator Correction
May 14, 2020
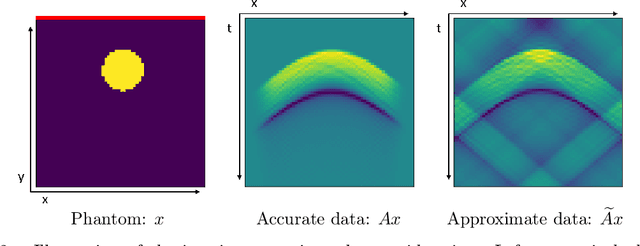

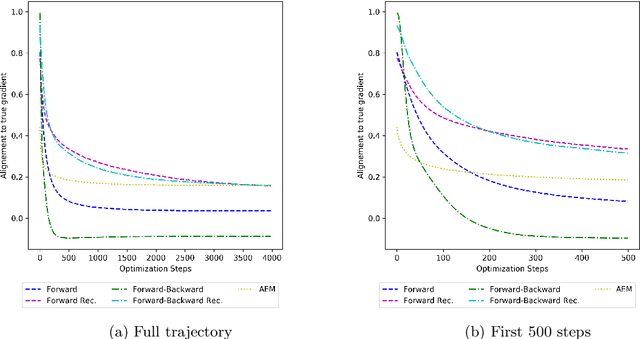
Abstract:We discuss the possibility to learn a data-driven explicit model correction for inverse problems and whether such a model correction can be used within a variational framework to obtain regularised reconstructions. This paper discusses the conceptual difficulty to learn such a forward model correction and proceeds to present a possible solution as forward-backward correction that explicitly corrects in both data and solution spaces. We then derive conditions under which solutions to the variational problem with a learned correction converge to solutions obtained with the correct operator. The proposed approach is evaluated on an application to limited view photoacoustic tomography and compared to the established framework of Bayesian approximation error method.
Inverse Graphics GAN: Learning to Generate 3D Shapes from Unstructured 2D Data
Feb 28, 2020

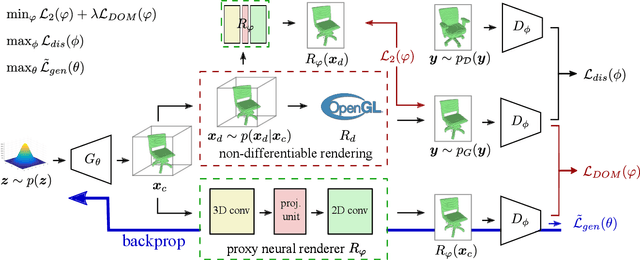

Abstract:Recent work has shown the ability to learn generative models for 3D shapes from only unstructured 2D images. However, training such models requires differentiating through the rasterization step of the rendering process, therefore past work has focused on developing bespoke rendering models which smooth over this non-differentiable process in various ways. Such models are thus unable to take advantage of the photo-realistic, fully featured, industrial renderers built by the gaming and graphics industry. In this paper we introduce the first scalable training technique for 3D generative models from 2D data which utilizes an off-the-shelf non-differentiable renderer. To account for the non-differentiability, we introduce a proxy neural renderer to match the output of the non-differentiable renderer. We further propose discriminator output matching to ensure that the neural renderer learns to smooth over the rasterization appropriately. We evaluate our model on images rendered from our generated 3D shapes, and show that our model can consistently learn to generate better shapes than existing models when trained with exclusively unstructured 2D images.
On the Connection Between Adversarial Robustness and Saliency Map Interpretability
May 10, 2019
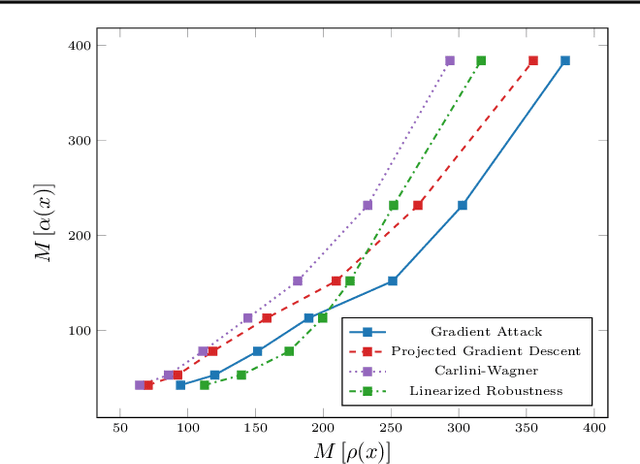
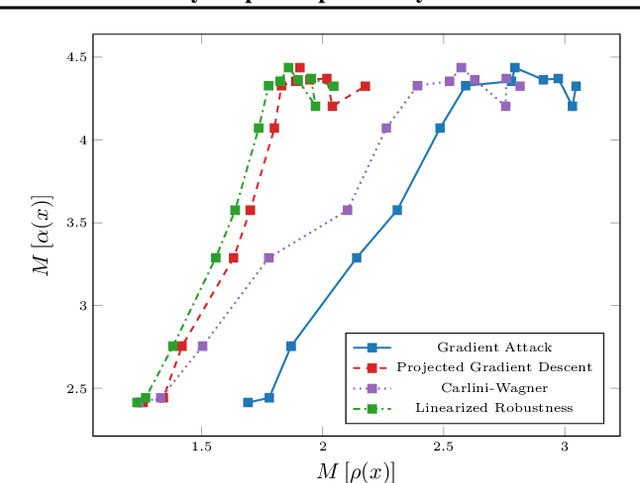
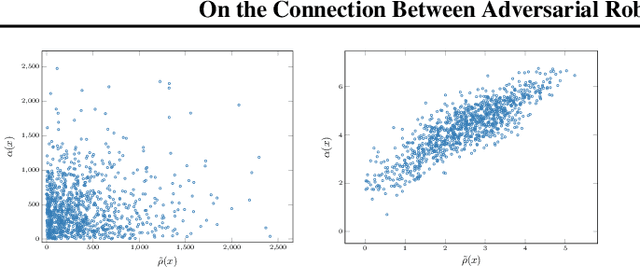
Abstract:Recent studies on the adversarial vulnerability of neural networks have shown that models trained to be more robust to adversarial attacks exhibit more interpretable saliency maps than their non-robust counterparts. We aim to quantify this behavior by considering the alignment between input image and saliency map. We hypothesize that as the distance to the decision boundary grows,so does the alignment. This connection is strictly true in the case of linear models. We confirm these theoretical findings with experiments based on models trained with a local Lipschitz regularization and identify where the non-linear nature of neural networks weakens the relation.
The Oracle of DLphi
Jan 27, 2019Abstract:We present a novel technique based on deep learning and set theory which yields exceptional classification and prediction results. Having access to a sufficiently large amount of labelled training data, our methodology is capable of predicting the labels of the test data almost always even if the training data is entirely unrelated to the test data. In other words, we prove in a specific setting that as long as one has access to enough data points, the quality of the data is irrelevant.
Task adapted reconstruction for inverse problems
Aug 27, 2018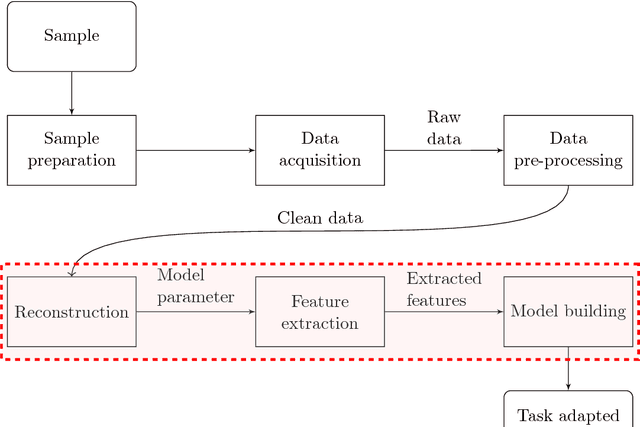
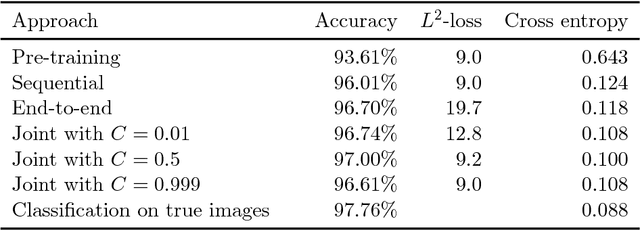
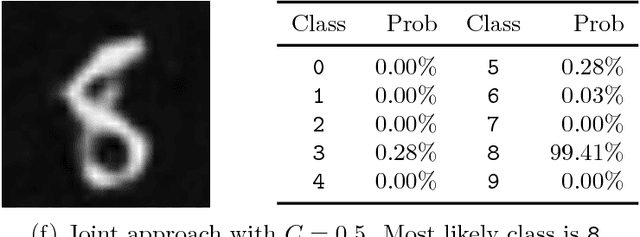
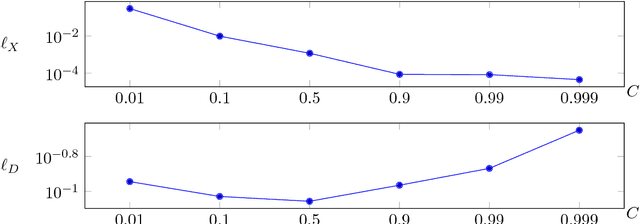
Abstract:The paper considers the problem of performing a task defined on a model parameter that is only observed indirectly through noisy data in an ill-posed inverse problem. A key aspect is to formalize the steps of reconstruction and task as appropriate estimators (non-randomized decision rules) in statistical estimation problems. The implementation makes use of (deep) neural networks to provide a differentiable parametrization of the family of estimators for both steps. These networks are combined and jointly trained against suitable supervised training data in order to minimize a joint differentiable loss function, resulting in an end-to-end task adapted reconstruction method. The suggested framework is generic, yet adaptable, with a plug-and-play structure for adjusting both the inverse problem and the task at hand. More precisely, the data model (forward operator and statistical model of the noise) associated with the inverse problem is exchangeable, e.g., by using neural network architecture given by a learned iterative method. Furthermore, any task that is encodable as a trainable neural network can be used. The approach is demonstrated on joint tomographic image reconstruction, classification and joint tomographic image reconstruction segmentation.
Banach Wasserstein GAN
Jun 18, 2018
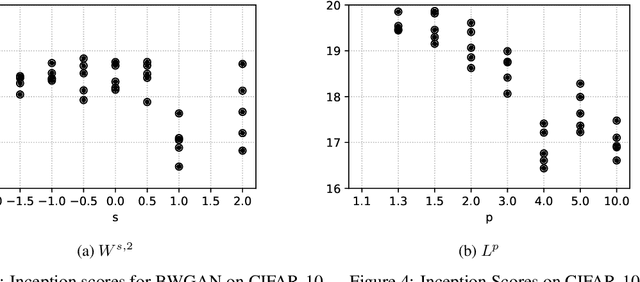
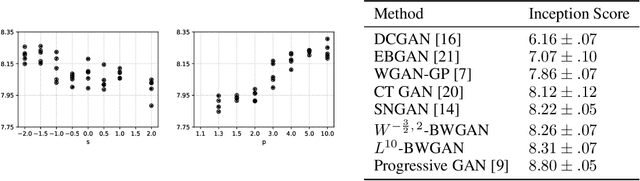
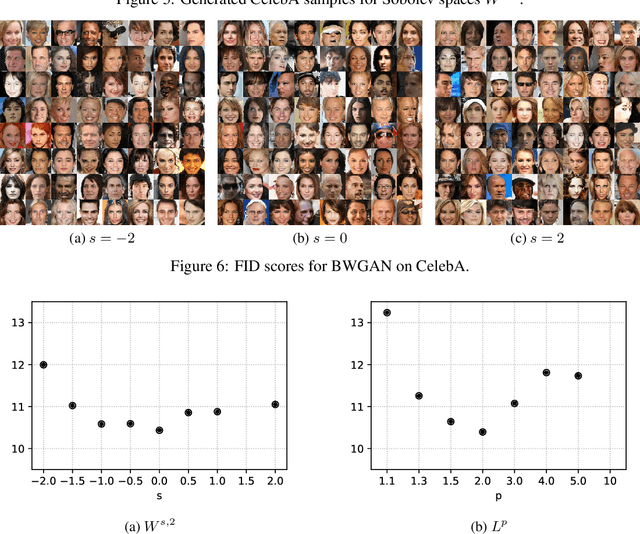
Abstract:Wasserstein Generative Adversarial Networks (WGANs) can be used to generate realistic samples from complicated image distributions. The Wasserstein metric used in WGANs is based on a notion of distance between individual images, which induces a notion of distance between probability distributions of images. So far the community has considered $\ell^2$ as the underlying distance. We generalize the theory of WGAN with gradient penalty to Banach spaces, allowing practitioners to select the features to emphasize in the generator. We further discuss the effect of some particular choices of underlying norms, focusing on Sobolev norms. Finally, we demonstrate the impact of the choice of norm on model performance and show state-of-the-art inception scores for non-progressive growing GANs on CIFAR-10.
Adversarial Regularizers in Inverse Problems
May 29, 2018

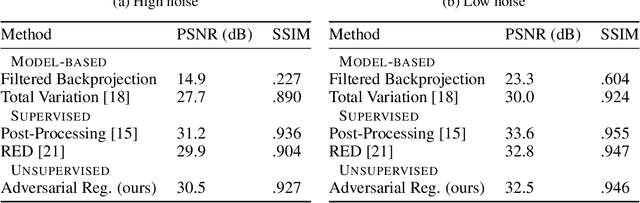
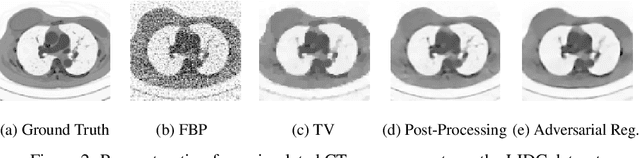
Abstract:Inverse Problems in medical imaging and computer vision are traditionally solved using purely model-based methods. Among those variational regularization models are one of the most popular approaches. We propose a new framework for applying data-driven approaches to inverse problems, using a neural network as a regularization functional. The network learns to discriminate between the distribution of ground truth images and the distribution of unregularized reconstructions. Once trained, the network is applied to the inverse problem by solving the corresponding variational problem. Unlike other data-based approaches for inverse problems, the algorithm can be applied even if only unsupervised training data is available. Experiments demonstrate the potential of the framework for denoising on the BSDS dataset and for computer tomography reconstruction on the LIDC dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge