Sarah J. Hamilton
Fast 3D Partial Boundary Data EIT Reconstructions using Direct Inversion CGO-based Methods
Dec 13, 2024
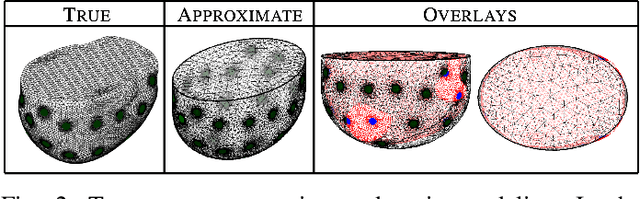
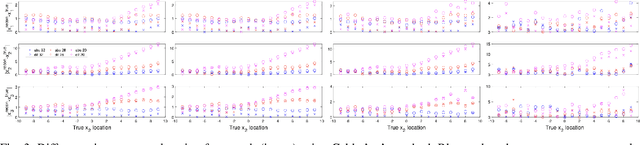
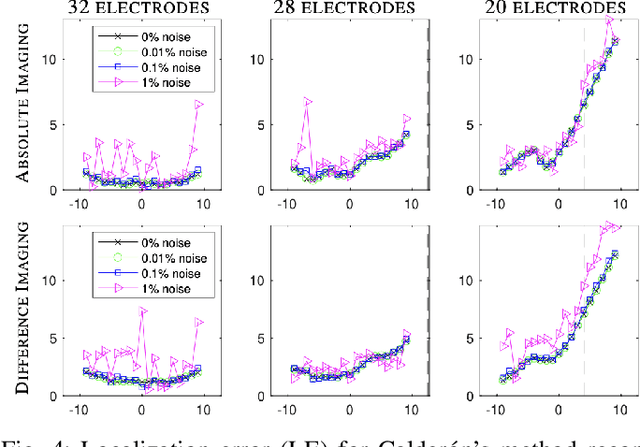
Abstract:The first partial boundary data complex geometrical optics based methods for electrical impedance tomography in three dimensions are developed, and tested, on simulated and experimental data. The methods provide good localization of targets for both absolute and time-difference imaging, when large portions of the domain are inaccessible for measurement. As most medical applications of electrical impedance tomography are limited to partial boundary data, the development of partial boundary algorithms is highly desirable. While iterative schemes have been used traditionally, their high computational cost makes them cost-prohibitive for applications that need fast imaging. The proposed algorithms require no iteration and provide informative absolute or time-difference images exceptionally quickly in under 2 seconds. Reconstructions are compared to reference reconstructions from standard linear difference imaging (30 seconds) and total variation regularized absolute imaging (several minutes) The algorithms perform well under high levels of noise and incorrect domain modeling.
Domain independent post-processing with graph U-nets: Applications to Electrical Impedance Tomographic Imaging
May 08, 2023Abstract:Reconstruction of tomographic images from boundary measurements requires flexibility with respect to target domains. For instance, when the system equations are modeled by partial differential equations the reconstruction is usually done on finite element (FE) meshes, allowing for flexible geometries. Thus, any processing of the obtained reconstructions should be ideally done on the FE mesh as well. For this purpose, we extend the hugely successful U-Net architecture that is limited to rectangular pixel or voxel domains to an equivalent that works flexibly on FE meshes. To achieve this, the FE mesh is converted into a graph and we formulate a graph U-Net with a new cluster pooling and unpooling on the graph that mimics the classic neighborhood based max-pooling. We demonstrate effectiveness and flexibility of the graph U-Net for improving reconstructions from electrical impedance tomographic (EIT) measurements, a nonlinear and highly ill-posed inverse problem. The performance is evaluated for simulated data and from three measurement devices with different measurement geometries and instrumentations. We successfully show that such networks can be trained with a simple two-dimensional simulated training set and generalize to very different domains, including measurements from a three-dimensional device and subsequent 3D reconstructions.
Graph Convolutional Networks for Model-Based Learning in Nonlinear Inverse Problems
Mar 28, 2021


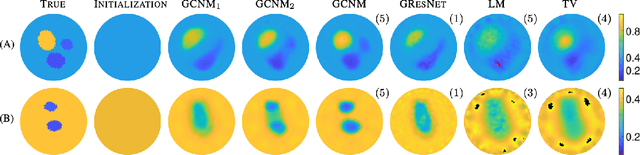
Abstract:The majority of model-based learned image reconstruction methods in medical imaging have been limited to uniform domains, such as pixelated images. If the underlying model is solved on nonuniform meshes, arising from a finite element method typical for nonlinear inverse problems, interpolation and embeddings are needed. To overcome this, we present a flexible framework to extend model-based learning directly to nonuniform meshes, by interpreting the mesh as a graph and formulating our network architectures using graph convolutional neural networks. This gives rise to the proposed iterative Graph Convolutional Newton's Method (GCNM), which directly includes the forward model into the solution of the inverse problem, while all updates are directly computed by the network on the problem specific mesh. We present results for Electrical Impedance Tomography, a severely ill-posed nonlinear inverse problem that is frequently solved via optimization-based methods, where the forward problem is solved by finite element methods. Results for absolute EIT imaging are compared to standard iterative methods as well as a graph residual network. We show that the GCNM has strong generalizability to different domain shapes, out of distribution data as well as experimental data, from purely simulated training data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge