Generation of patient specific cardiac chamber models using generative neural networks under a Bayesian framework for electroanatomical mapping

Electroanatomical mapping is a technique used in cardiology to create a detailed 3D map of the electrical activity in the heart. It is useful for diagnosis, treatment planning and real time guidance in cardiac ablation procedures to treat arrhythmias like atrial fibrillation. A probabilistic machine learning model trained on a library of CT/MRI scans of the heart can be used during electroanatomical mapping to generate a patient-specific 3D model of the chamber being mapped. The use of probabilistic machine learning models under a Bayesian framework provides a way to quantify uncertainty in results and provide a natural framework of interpretability of the model. Here we introduce a Bayesian approach to surface reconstruction of cardiac chamber models from a sparse 3D point cloud data acquired during electroanatomical mapping. We show how probabilistic graphical models trained on segmented CT/MRI data can be used to generate cardiac chamber models from few acquired locations thereby reducing procedure time and x-ray exposure. We show how they provide insight into what the neural network learns from the segmented CT/MRI images used to train the network, which provides explainability to the resulting cardiac chamber models generated by the model.

Pruning a neural network using Bayesian inference

Neural network pruning is a highly effective technique aimed at reducing the computational and memory demands of large neural networks. In this research paper, we present a novel approach to pruning neural networks utilizing Bayesian inference, which can seamlessly integrate into the training procedure. Our proposed method leverages the posterior probabilities of the neural network prior to and following pruning, enabling the calculation of Bayes factors. The calculated Bayes factors guide the iterative pruning. Through comprehensive evaluations conducted on multiple benchmarks, we demonstrate that our method achieves desired levels of sparsity while maintaining competitive accuracy.

Graph Convolutional Networks for Model-Based Learning in Nonlinear Inverse Problems

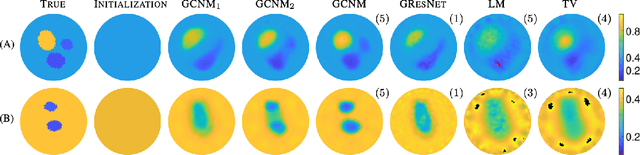
The majority of model-based learned image reconstruction methods in medical imaging have been limited to uniform domains, such as pixelated images. If the underlying model is solved on nonuniform meshes, arising from a finite element method typical for nonlinear inverse problems, interpolation and embeddings are needed. To overcome this, we present a flexible framework to extend model-based learning directly to nonuniform meshes, by interpreting the mesh as a graph and formulating our network architectures using graph convolutional neural networks. This gives rise to the proposed iterative Graph Convolutional Newton's Method (GCNM), which directly includes the forward model into the solution of the inverse problem, while all updates are directly computed by the network on the problem specific mesh. We present results for Electrical Impedance Tomography, a severely ill-posed nonlinear inverse problem that is frequently solved via optimization-based methods, where the forward problem is solved by finite element methods. Results for absolute EIT imaging are compared to standard iterative methods as well as a graph residual network. We show that the GCNM has strong generalizability to different domain shapes, out of distribution data as well as experimental data, from purely simulated training data.