Fast 3D Partial Boundary Data EIT Reconstructions using Direct Inversion CGO-based Methods

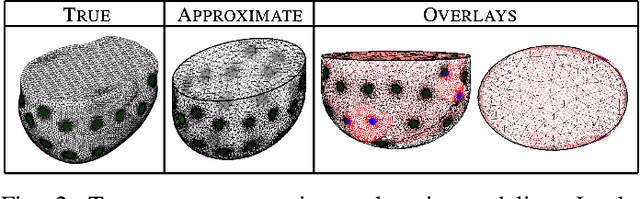
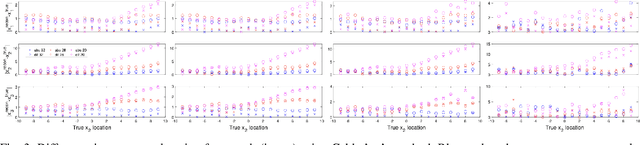
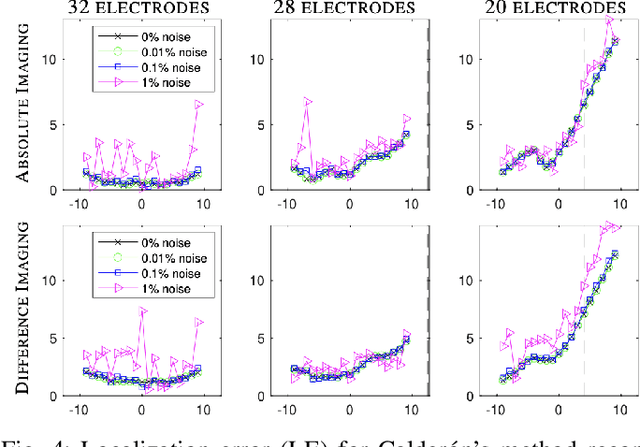
The first partial boundary data complex geometrical optics based methods for electrical impedance tomography in three dimensions are developed, and tested, on simulated and experimental data. The methods provide good localization of targets for both absolute and time-difference imaging, when large portions of the domain are inaccessible for measurement. As most medical applications of electrical impedance tomography are limited to partial boundary data, the development of partial boundary algorithms is highly desirable. While iterative schemes have been used traditionally, their high computational cost makes them cost-prohibitive for applications that need fast imaging. The proposed algorithms require no iteration and provide informative absolute or time-difference images exceptionally quickly in under 2 seconds. Reconstructions are compared to reference reconstructions from standard linear difference imaging (30 seconds) and total variation regularized absolute imaging (several minutes) The algorithms perform well under high levels of noise and incorrect domain modeling.

Embedded quantitative MRI T1rho mapping using non-linear primal-dual proximal splitting

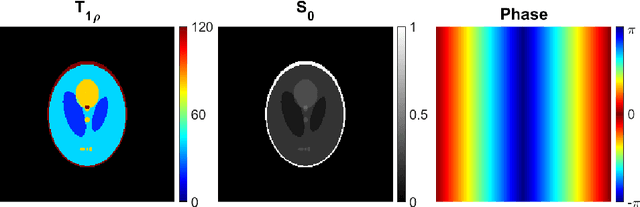
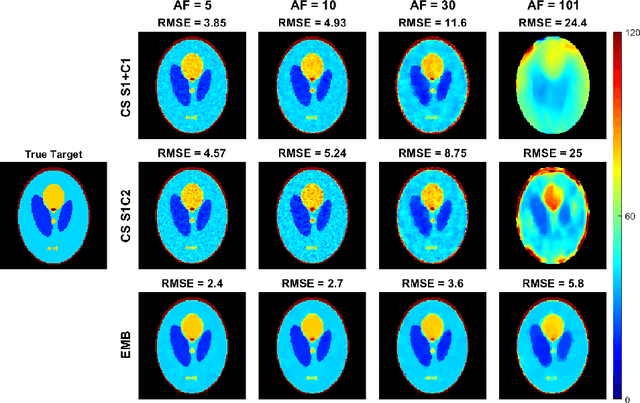
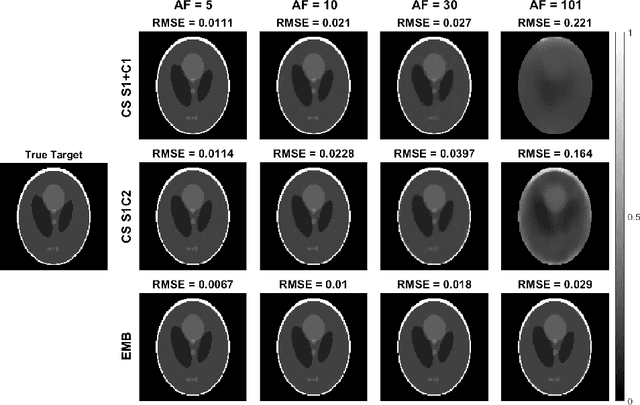
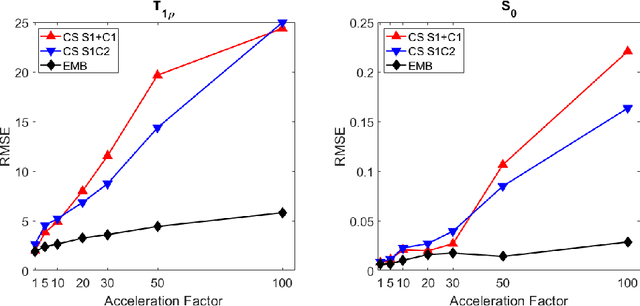
Quantitative MRI (qMRI) methods allow reducing the subjectivity of clinical MRI by providing numerical values on which diagnostic assessment or predictions of tissue properties can be based. However, qMRI measurements typically take more time than anatomical imaging due to requiring multiple measurements with varying contrasts for, e.g., relaxation time mapping. To reduce the scanning time, undersampled data may be combined with compressed sensing reconstruction techniques. Typical CS reconstructions first reconstruct a complex-valued set of images corresponding to the varying contrasts, followed by a non-linear signal model fit to obtain the parameter maps. We propose a direct, embedded reconstruction method for T1rho mapping. The proposed method capitalizes on a known signal model to directly reconstruct the desired parameter map using a non-linear optimization model. The proposed reconstruction method also allows directly regularizing the parameter map of interest, and greatly reduces the number of unknowns in the reconstruction. We test the proposed model using a simulated radially sampled data from a 2D phantom and 2D cartesian ex vivo measurements of a mouse kidney specimen. We compare the embedded reconstruction model to two CS reconstruction models, and in the cartesian test case also iFFT. The proposed, embedded model outperformed the reference methods on both test cases, especially with higher acceleration factors.