Metric Learning for Clifford Group Equivariant Neural Networks

Clifford Group Equivariant Neural Networks (CGENNs) leverage Clifford algebras and multivectors as an alternative approach to incorporating group equivariance to ensure symmetry constraints in neural representations. In principle, this formulation generalizes to orthogonal groups and preserves equivariance regardless of the metric signature. However, previous works have restricted internal network representations to Euclidean or Minkowski (pseudo-)metrics, handpicked depending on the problem at hand. In this work, we propose an alternative method that enables the metric to be learned in a data-driven fashion, allowing the CGENN network to learn more flexible representations. Specifically, we populate metric matrices fully, ensuring they are symmetric by construction, and leverage eigenvalue decomposition to integrate this additional learnable component into the original CGENN formulation in a principled manner. Additionally, we motivate our method using insights from category theory, which enables us to explain Clifford algebras as a categorical construction and guarantee the mathematical soundness of our approach. We validate our method in various tasks and showcase the advantages of learning more flexible latent metric representations. The code and data are available at https://github.com/rick-ali/Metric-Learning-for-CGENNs

Improving Antibody Design with Force-Guided Sampling in Diffusion Models

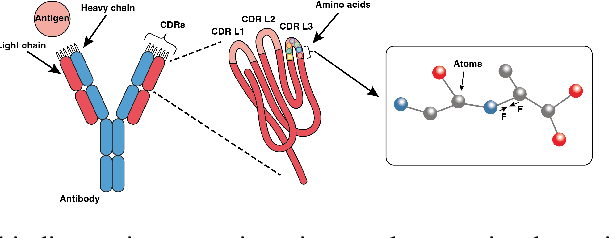
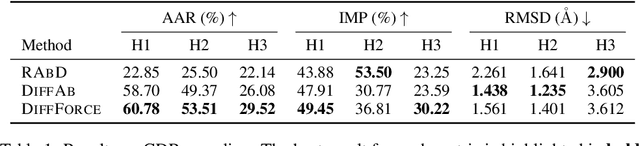
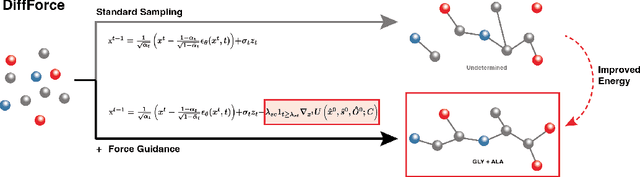
Antibodies, crucial for immune defense, primarily rely on complementarity-determining regions (CDRs) to bind and neutralize antigens, such as viruses. The design of these CDRs determines the antibody's affinity and specificity towards its target. Generative models, particularly denoising diffusion probabilistic models (DDPMs), have shown potential to advance the structure-based design of CDR regions. However, only a limited dataset of bound antibody-antigen structures is available, and generalization to out-of-distribution interfaces remains a challenge. Physics based force-fields, which approximate atomic interactions, offer a coarse but universal source of information to better mold designs to target interfaces. Integrating this foundational information into diffusion models is, therefore, highly desirable. Here, we propose a novel approach to enhance the sampling process of diffusion models by integrating force field energy-based feedback. Our model, DiffForce, employs forces to guide the diffusion sampling process, effectively blending the two distributions. Through extensive experiments, we demonstrate that our method guides the model to sample CDRs with lower energy, enhancing both the structure and sequence of the generated antibodies.