Permutation Picture of Graph Combinatorial Optimization Problems

This paper proposes a framework that formulates a wide range of graph combinatorial optimization problems using permutation-based representations. These problems include the travelling salesman problem, maximum independent set, maximum cut, and various other related problems. This work potentially opens up new avenues for algorithm design in neural combinatorial optimization, bridging the gap between discrete and continuous optimization techniques.

Comment on paper: Position: Rethinking Post-Hoc Search-Based Neural Approaches for Solving Large-Scale Traveling Salesman Problems

We identify two major issues in the SoftDist paper (Xia et al.): (1) the failure to run all steps of different baselines on the same hardware environment, and (2) the use of inconsistent time measurements when comparing to other baselines. These issues lead to flawed conclusions. When all steps are executed in the same hardware environment, the primary claim made in SoftDist is no longer supported.

On Size and Hardness Generalization in Unsupervised Learning for the Travelling Salesman Problem

We study the generalization capability of Unsupervised Learning in solving the Travelling Salesman Problem (TSP). We use a Graph Neural Network (GNN) trained with a surrogate loss function to generate an embedding for each node. We use these embeddings to construct a heat map that indicates the likelihood of each edge being part of the optimal route. We then apply local search to generate our final predictions. Our investigation explores how different training instance sizes, embedding dimensions, and distributions influence the outcomes of Unsupervised Learning methods. Our results show that training with larger instance sizes and increasing embedding dimensions can build a more effective representation, enhancing the model's ability to solve TSP. Furthermore, in evaluating generalization across different distributions, we first determine the hardness of various distributions and explore how different hardnesses affect the final results. Our findings suggest that models trained on harder instances exhibit better generalization capabilities, highlighting the importance of selecting appropriate training instances in solving TSP using Unsupervised Learning.

Unsupervised Learning for Solving the Travelling Salesman Problem

We propose UTSP, an unsupervised learning (UL) framework for solving the Travelling Salesman Problem (TSP). We train a Graph Neural Network (GNN) using a surrogate loss. The GNN outputs a heat map representing the probability for each edge to be part of the optimal path. We then apply local search to generate our final prediction based on the heat map. Our loss function consists of two parts: one pushes the model to find the shortest path and the other serves as a surrogate for the constraint that the route should form a Hamiltonian Cycle. Experimental results show that UTSP outperforms the existing data-driven TSP heuristics. Our approach is parameter efficient as well as data efficient: the model takes $\sim$ 10\% of the number of parameters and $\sim$ 0.2\% of training samples compared with reinforcement learning or supervised learning methods.

Can Hybrid Geometric Scattering Networks Help Solve the Maximal Clique Problem?

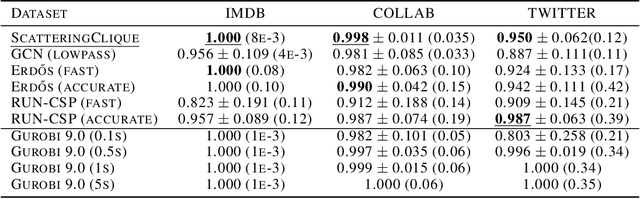
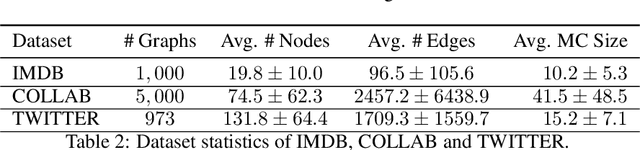
We propose a geometric scattering-based graph neural network (GNN) for approximating solutions of the NP-hard maximal clique (MC) problem. We construct a loss function with two terms, one which encourages the network to find a large set of nodes and the other which acts as a surrogate for the constraint that the nodes form a clique. We then use this loss to train a novel GNN architecture that outputs a vector representing the probability for each node to be part of the MC and apply a rule-based decoder to make our final prediction. The incorporation of the scattering transform alleviates the so-called oversmoothing problem that is often encountered in GNNs and would degrade the performance of our proposed setup. Our empirical results demonstrate that our method outperforms representative GNN baselines in terms of solution accuracy and inference speed as well as conventional solvers like GUROBI with limited time budgets.

Overcoming Oversmoothness in Graph Convolutional Networks via Hybrid Scattering Networks

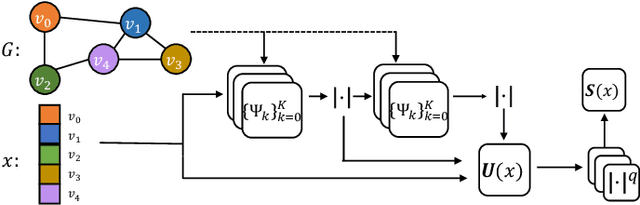
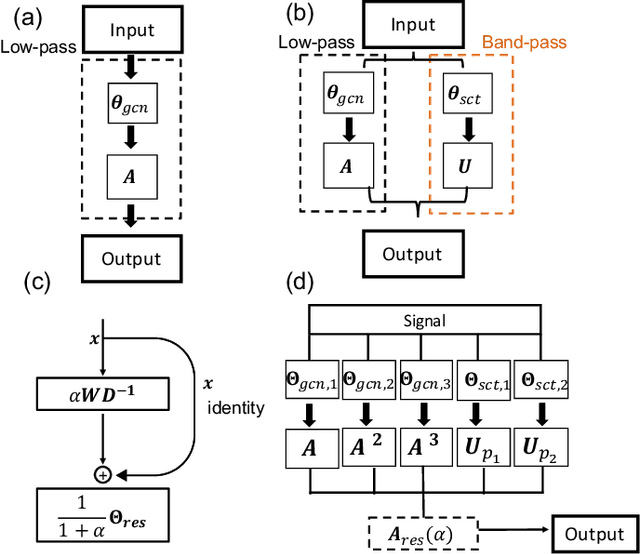
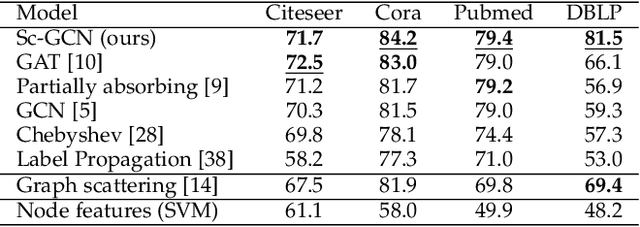
Geometric deep learning (GDL) has made great strides towards generalizing the design of structure-aware neural network architectures from traditional domains to non-Euclidean ones, such as graphs. This gave rise to graph neural network (GNN) models that can be applied to graph-structured datasets arising, for example, in social networks, biochemistry, and material science. Graph convolutional networks (GCNs) in particular, inspired by their Euclidean counterparts, have been successful in processing graph data by extracting structure-aware features. However, current GNN models (and GCNs in particular) are known to be constrained by various phenomena that limit their expressive power and ability to generalize to more complex graph datasets. Most models essentially rely on low-pass filtering of graph signals via local averaging operations, thus leading to oversmoothing. Here, we propose a hybrid GNN framework that combines traditional GCN filters with band-pass filters defined via the geometric scattering transform. We further introduce an attention framework that allows the model to locally attend over the combined information from different GNN filters at the node level. Our theoretical results establish the complementary benefits of the scattering filters to leverage structural information from the graph, while our experiments show the benefits of our method on various learning tasks.

Geometric Scattering Attention Networks

Geometric scattering has recently gained recognition in graph representation learning, and recent work has shown that integrating scattering features in graph convolution networks (GCNs) can alleviate the typical oversmoothing of features in node representation learning. However, scattering methods often rely on handcrafted design, requiring careful selection of frequency bands via a cascade of wavelet transforms, as well as an effective weight sharing scheme to combine together low- and band-pass information. Here, we introduce a new attention-based architecture to produce adaptive task-driven node representations by implicitly learning node-wise weights for combining multiple scattering and GCN channels in the network. We show the resulting geometric scattering attention network (GSAN) outperforms previous networks in semi-supervised node classification, while also enabling a spectral study of extracted information by examining node-wise attention weights.

Persistent Neurons

Most algorithms used in neural networks(NN)-based leaning tasks are strongly affected by the choices of initialization. Good initialization can avoid sub-optimal solutions and alleviate saturation during training. However, designing improved initialization strategies is a difficult task and our understanding of good initialization is still very primitive. Here, we propose persistent neurons, a strategy that optimizes the learning trajectory using information from previous converged solutions. More precisely, we let the parameters explore new landscapes by penalizing the model from converging to the previous solutions under the same initialization. Specifically, we show that persistent neurons, under certain data distribution, is able to converge to more optimal solutions while initializations under popular framework find bad local minima. We further demonstrate that persistent neurons helps improve the model's performance under both good and poor initializations. Moreover, we evaluate full and partial persistent model and show it can be used to boost the performance on a range of NN structures, such as AlexNet and residual neural network. Saturation of activation functions during persistent training is also studied.

Scattering GCN: Overcoming Oversmoothness in Graph Convolutional Networks

Graph convolutional networks (GCNs) have shown promising results in processing graph data by extracting structure-aware features. This gave rise to extensive work in geometric deep learning, focusing on designing network architectures that ensure neuron activations conform to regularity patterns within the input graph. However, in most cases the graph structure is only accounted for by considering the similarity of activations between adjacent nodes, which in turn degrades the results. In this work, we augment GCN models by incorporating richer notions of regularity by leveraging cascades of band-pass filters, known as geometric scatterings. The produced graph features incorporate multiscale representations of local graph structures, while avoiding overly smooth activations forced by previous architectures. Moreover, inspired by skip connections used in residual networks, we introduce graph residual convolutions that reduce high-frequency noise caused by joining together information at multiple scales. Our hybrid architecture introduces a new model for semi-supervised learning on graph-structured data, and its potential is demonstrated for node classification tasks on multiple graph datasets, where it outperforms leading GCN models.

Predicting ice flow using machine learning

Though machine learning has achieved notable success in modeling sequential and spatial data for speech recognition and in computer vision, applications to remote sensing and climate science problems are seldom considered. In this paper, we demonstrate techniques from unsupervised learning of future video frame prediction, to increase the accuracy of ice flow tracking in multi-spectral satellite images. As the volume of cryosphere data increases in coming years, this is an interesting and important opportunity for machine learning to address a global challenge for climate change, risk management from floods, and conserving freshwater resources. Future frame prediction of ice melt and tracking the optical flow of ice dynamics presents modeling difficulties, due to uncertainties in global temperature increase, changing precipitation patterns, occlusion from cloud cover, rapid melting and glacier retreat due to black carbon aerosol deposition, from wildfires or human fossil emissions. We show the adversarial learning method helps improve the accuracy of tracking the optical flow of ice dynamics compared to existing methods in climate science. We present a dataset, IceNet, to encourage machine learning research and to help facilitate further applications in the areas of cryospheric science and climate change.