Overcoming Oversmoothness in Graph Convolutional Networks via Hybrid Scattering Networks

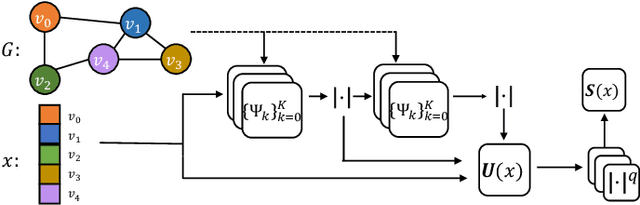
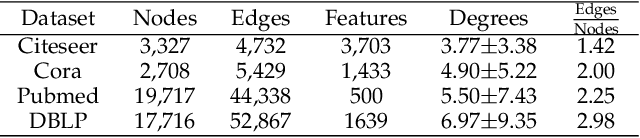
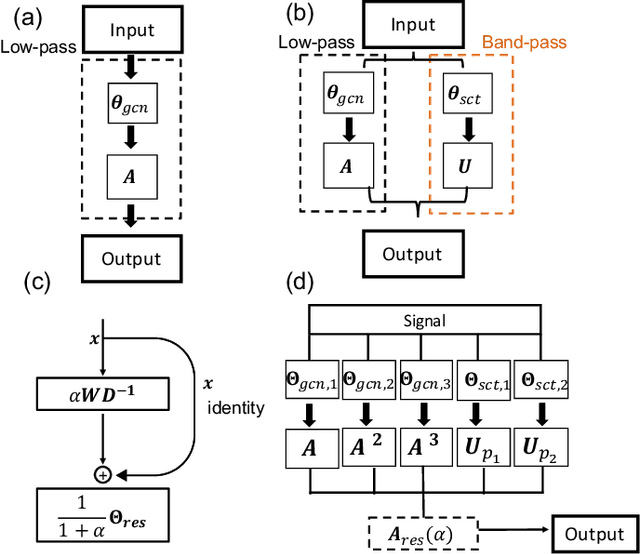
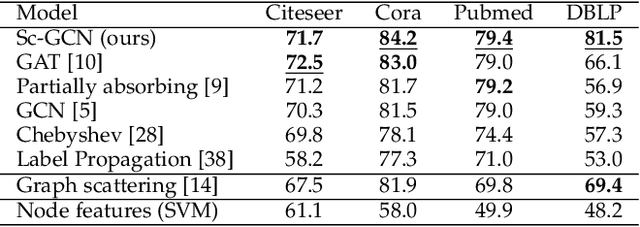
Geometric deep learning (GDL) has made great strides towards generalizing the design of structure-aware neural network architectures from traditional domains to non-Euclidean ones, such as graphs. This gave rise to graph neural network (GNN) models that can be applied to graph-structured datasets arising, for example, in social networks, biochemistry, and material science. Graph convolutional networks (GCNs) in particular, inspired by their Euclidean counterparts, have been successful in processing graph data by extracting structure-aware features. However, current GNN models (and GCNs in particular) are known to be constrained by various phenomena that limit their expressive power and ability to generalize to more complex graph datasets. Most models essentially rely on low-pass filtering of graph signals via local averaging operations, thus leading to oversmoothing. Here, we propose a hybrid GNN framework that combines traditional GCN filters with band-pass filters defined via the geometric scattering transform. We further introduce an attention framework that allows the model to locally attend over the combined information from different GNN filters at the node level. Our theoretical results establish the complementary benefits of the scattering filters to leverage structural information from the graph, while our experiments show the benefits of our method on various learning tasks.