A Dual Perspective on Decision-Focused Learning: Scalable Training via Dual-Guided Surrogates

Many real-world decisions are made under uncertainty by solving optimization problems using predicted quantities. This predict-then-optimize paradigm has motivated decision-focused learning, which trains models with awareness of how the optimizer uses predictions, improving the performance of downstream decisions. Despite its promise, scaling is challenging: state-of-the-art methods either differentiate through a solver or rely on task-specific surrogates, both of which require frequent and expensive calls to an optimizer, often a combinatorial one. In this paper, we leverage dual variables from the downstream problem to shape learning and introduce Dual-Guided Loss (DGL), a simple, scalable objective that preserves decision alignment while reducing solver dependence. We construct DGL specifically for combinatorial selection problems with natural one-of-many constraints, such as matching, knapsack, and shortest path. Our approach (a) decouples optimization from gradient updates by solving the downstream problem only periodically; (b) between refreshes, trains on dual-adjusted targets using simple differentiable surrogate losses; and (c) as refreshes become less frequent, drives training cost toward standard supervised learning while retaining strong decision alignment. We prove that DGL has asymptotically diminishing decision regret, analyze runtime complexity, and show on two problem classes that DGL matches or exceeds state-of-the-art DFL methods while using far fewer solver calls and substantially less training time. Code is available at https://github.com/paularodr/Dual-Guided-Learning.

Optimizing Vital Sign Monitoring in Resource-Constrained Maternal Care: An RL-Based Restless Bandit Approach

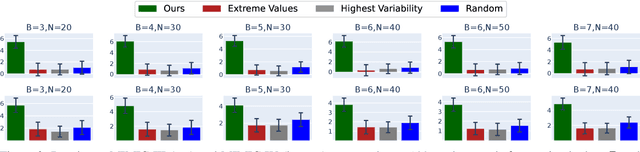
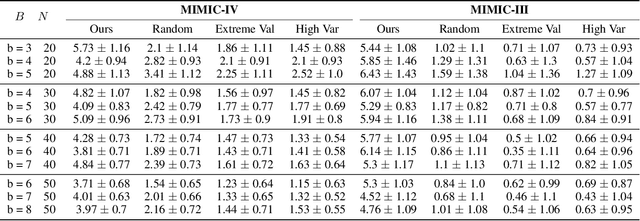
Maternal mortality remains a significant global public health challenge. One promising approach to reducing maternal deaths occurring during facility-based childbirth is through early warning systems, which require the consistent monitoring of mothers' vital signs after giving birth. Wireless vital sign monitoring devices offer a labor-efficient solution for continuous monitoring, but their scarcity raises the critical question of how to allocate them most effectively. We devise an allocation algorithm for this problem by modeling it as a variant of the popular Restless Multi-Armed Bandit (RMAB) paradigm. In doing so, we identify and address novel, previously unstudied constraints unique to this domain, which render previous approaches for RMABs unsuitable and significantly increase the complexity of the learning and planning problem. To overcome these challenges, we adopt the popular Proximal Policy Optimization (PPO) algorithm from reinforcement learning to learn an allocation policy by training a policy and value function network. We demonstrate in simulations that our approach outperforms the best heuristic baseline by up to a factor of $4$.

What is the Right Notion of Distance between Predict-then-Optimize Tasks?

Comparing datasets is a fundamental task in machine learning, essential for various learning paradigms; from evaluating train and test datasets for model generalization to using dataset similarity for detecting data drift. While traditional notions of dataset distances offer principled measures of similarity, their utility has largely been assessed through prediction error minimization. However, in Predict-then-Optimize (PtO) frameworks, where predictions serve as inputs for downstream optimization tasks, model performance is measured through decision regret minimization rather than prediction error minimization. In this work, we (i) show that traditional dataset distances, which rely solely on feature and label dimensions, lack informativeness in the PtO context, and (ii) propose a new dataset distance that incorporates the impacts of downstream decisions. Our results show that this decision-aware dataset distance effectively captures adaptation success in PtO contexts, providing a PtO adaptation bound in terms of dataset distance. Empirically, we show that our proposed distance measure accurately predicts transferability across three different PtO tasks from the literature.