A Mathematical Framework for AI-Human Integration in Work

The rapid rise of Generative AI (GenAI) tools has sparked debate over their role in complementing or replacing human workers across job contexts. We present a mathematical framework that models jobs, workers, and worker-job fit, introducing a novel decomposition of skills into decision-level and action-level subskills to reflect the complementary strengths of humans and GenAI. We analyze how changes in subskill abilities affect job success, identifying conditions for sharp transitions in success probability. We also establish sufficient conditions under which combining workers with complementary subskills significantly outperforms relying on a single worker. This explains phenomena such as productivity compression, where GenAI assistance yields larger gains for lower-skilled workers. We demonstrate the framework' s practicality using data from O*NET and Big-Bench Lite, aligning real-world data with our model via subskill-division methods. Our results highlight when and how GenAI complements human skills, rather than replacing them.

The Role of Diversity in In-Context Learning for Large Language Models

In-context learning (ICL) is a crucial capability of current large language models (LLMs), where the selection of examples plays a key role in performance. While most existing approaches focus on selecting the most similar examples to the query, the impact of diversity in example selection remains underexplored. We systematically investigate the role of diversity in in-context example selection through experiments across a range of tasks, from sentiment classification to more challenging math and code problems. Experiments on Llama-3.1, Gemma-2, and Mistral-v0.3 families of models show that diversity-aware selection methods improve performance, particularly on complex tasks like math and code, and enhance robustness to out-of-distribution queries. To support these findings, we introduce a theoretical framework that explains the benefits of incorporating diversity in in-context example selection.

MuraNet: Multi-task Floor Plan Recognition with Relation Attention

The recognition of information in floor plan data requires the use of detection and segmentation models. However, relying on several single-task models can result in ineffective utilization of relevant information when there are multiple tasks present simultaneously. To address this challenge, we introduce MuraNet, an attention-based multi-task model for segmentation and detection tasks in floor plan data. In MuraNet, we adopt a unified encoder called MURA as the backbone with two separated branches: an enhanced segmentation decoder branch and a decoupled detection head branch based on YOLOX, for segmentation and detection tasks respectively. The architecture of MuraNet is designed to leverage the fact that walls, doors, and windows usually constitute the primary structure of a floor plan's architecture. By jointly training the model on both detection and segmentation tasks, we believe MuraNet can effectively extract and utilize relevant features for both tasks. Our experiments on the CubiCasa5k public dataset show that MuraNet improves convergence speed during training compared to single-task models like U-Net and YOLOv3. Moreover, we observe improvements in the average AP and IoU in detection and segmentation tasks, respectively.Our ablation experiments demonstrate that the attention-based unified backbone of MuraNet achieves better feature extraction in floor plan recognition tasks, and the use of decoupled multi-head branches for different tasks further improves model performance. We believe that our proposed MuraNet model can address the disadvantages of single-task models and improve the accuracy and efficiency of floor plan data recognition.

A Hierarchical Destroy and Repair Approach for Solving Very Large-Scale Travelling Salesman Problem

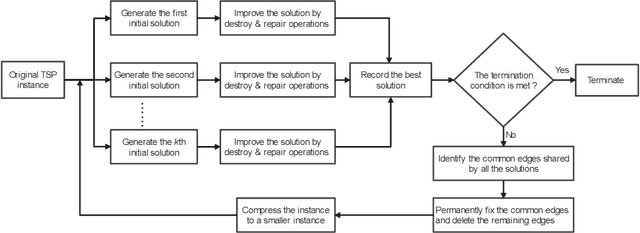
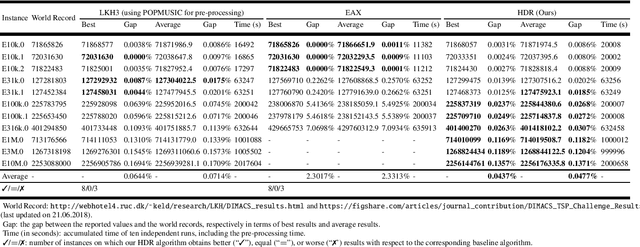
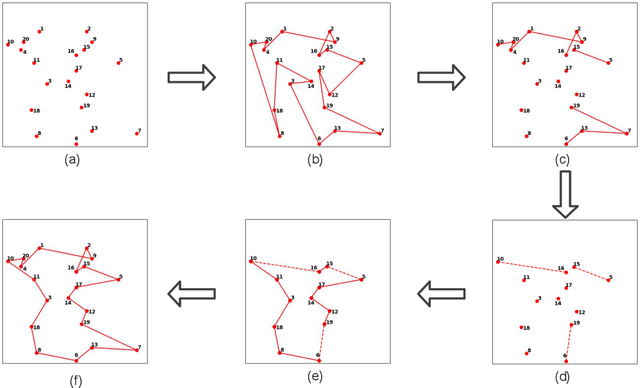
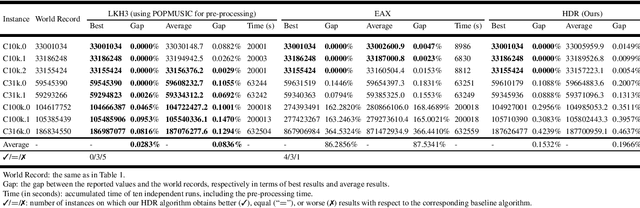
For prohibitively large-scale Travelling Salesman Problems (TSPs), existing algorithms face big challenges in terms of both computational efficiency and solution quality. To address this issue, we propose a hierarchical destroy-and-repair (HDR) approach, which attempts to improve an initial solution by applying a series of carefully designed destroy-and-repair operations. A key innovative concept is the hierarchical search framework, which recursively fixes partial edges and compresses the input instance into a small-scale TSP under some equivalence guarantee. This neat search framework is able to deliver highly competitive solutions within a reasonable time. Fair comparisons based on nineteen famous large-scale instances (with 10,000 to 10,000,000 cities) show that HDR is highly competitive against existing state-of-the-art TSP algorithms, in terms of both efficiency and solution quality. Notably, on two large instances with 3,162,278 and 10,000,000 cities, HDR breaks the world records (i.e., best-known results regardless of computation time), which were previously achieved by LKH and its variants, while HDR is completely independent of LKH. Finally, ablation studies are performed to certify the importance and validity of the hierarchical search framework.

Subset Selection Based On Multiple Rankings in the Presence of Bias: Effectiveness of Fairness Constraints for Multiwinner Voting Score Functions

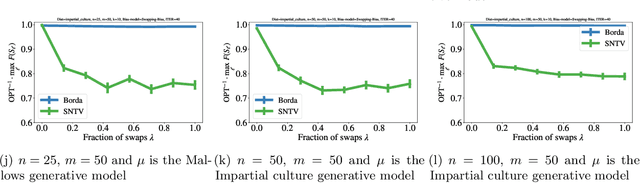
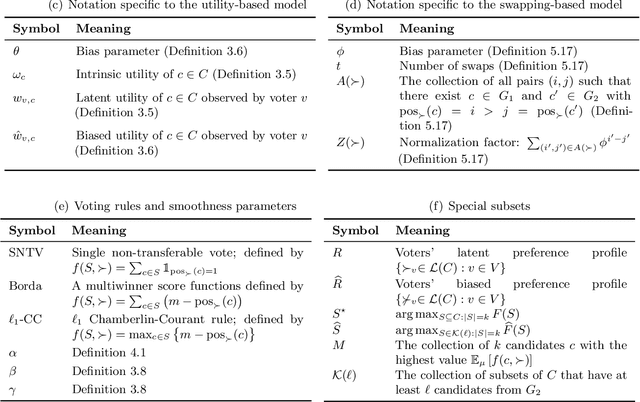
We consider the problem of subset selection where one is given multiple rankings of items and the goal is to select the highest ``quality'' subset. Score functions from the multiwinner voting literature have been used to aggregate rankings into quality scores for subsets. We study this setting of subset selection problems when, in addition, rankings may contain systemic or unconscious biases toward a group of items. For a general model of input rankings and biases, we show that requiring the selected subset to satisfy group fairness constraints can improve the quality of the selection with respect to unbiased rankings. Importantly, we show that for fairness constraints to be effective, different multiwinner score functions may require a drastically different number of rankings: While for some functions, fairness constraints need an exponential number of rankings to recover a close-to-optimal solution, for others, this dependency is only polynomial. This result relies on a novel notion of ``smoothness'' of submodular functions in this setting that quantifies how well a function can ``correctly'' assess the quality of items in the presence of bias. The results in this paper can be used to guide the choice of multiwinner score functions for the subset selection setting considered here; we additionally provide a tool to empirically enable this.

Coresets for Vertical Federated Learning: Regularized Linear Regression and $K$-Means Clustering

Vertical federated learning (VFL), where data features are stored in multiple parties distributively, is an important area in machine learning. However, the communication complexity for VFL is typically very high. In this paper, we propose a unified framework by constructing coresets in a distributed fashion for communication-efficient VFL. We study two important learning tasks in the VFL setting: regularized linear regression and $k$-means clustering, and apply our coreset framework to both problems. We theoretically show that using coresets can drastically alleviate the communication complexity, while nearly maintain the solution quality. Numerical experiments are conducted to corroborate our theoretical findings.

A Roadmap for Big Model

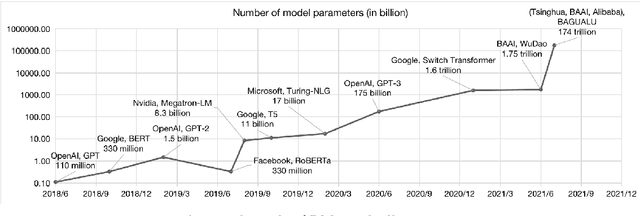
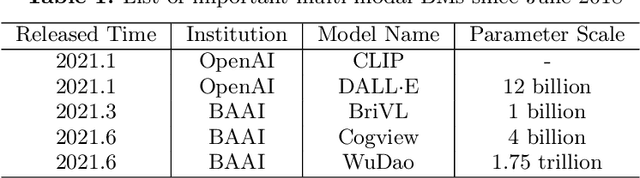
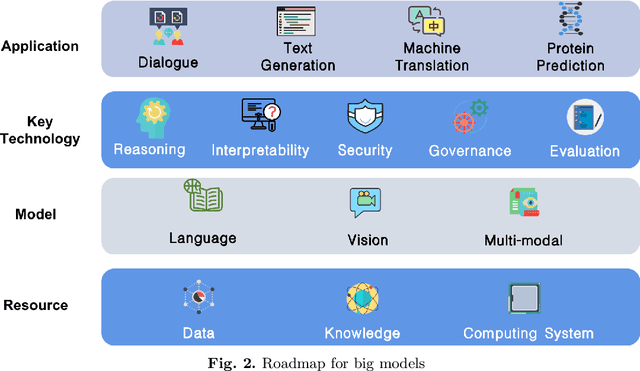
With the rapid development of deep learning, training Big Models (BMs) for multiple downstream tasks becomes a popular paradigm. Researchers have achieved various outcomes in the construction of BMs and the BM application in many fields. At present, there is a lack of research work that sorts out the overall progress of BMs and guides the follow-up research. In this paper, we cover not only the BM technologies themselves but also the prerequisites for BM training and applications with BMs, dividing the BM review into four parts: Resource, Models, Key Technologies and Application. We introduce 16 specific BM-related topics in those four parts, they are Data, Knowledge, Computing System, Parallel Training System, Language Model, Vision Model, Multi-modal Model, Theory&Interpretability, Commonsense Reasoning, Reliability&Security, Governance, Evaluation, Machine Translation, Text Generation, Dialogue and Protein Research. In each topic, we summarize clearly the current studies and propose some future research directions. At the end of this paper, we conclude the further development of BMs in a more general view.

Coresets for Time Series Clustering

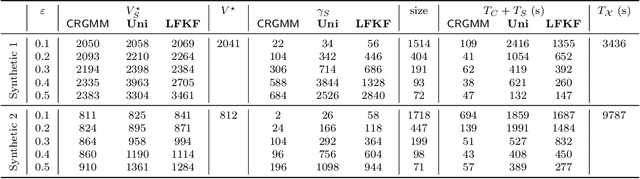
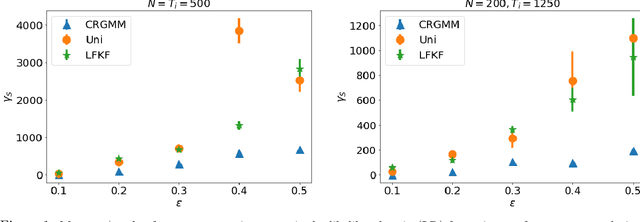
We study the problem of constructing coresets for clustering problems with time series data. This problem has gained importance across many fields including biology, medicine, and economics due to the proliferation of sensors facilitating real-time measurement and rapid drop in storage costs. In particular, we consider the setting where the time series data on $N$ entities is generated from a Gaussian mixture model with autocorrelations over $k$ clusters in $\mathbb{R}^d$. Our main contribution is an algorithm to construct coresets for the maximum likelihood objective for this mixture model. Our algorithm is efficient, and under a mild boundedness assumption on the covariance matrices of the underlying Gaussians, the size of the coreset is independent of the number of entities $N$ and the number of observations for each entity, and depends only polynomially on $k$, $d$ and $1/\varepsilon$, where $\varepsilon$ is the error parameter. We empirically assess the performance of our coreset with synthetic data.

CAC: A Clustering Based Framework for Classification

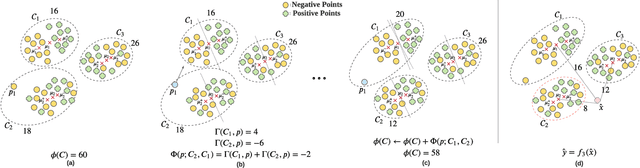
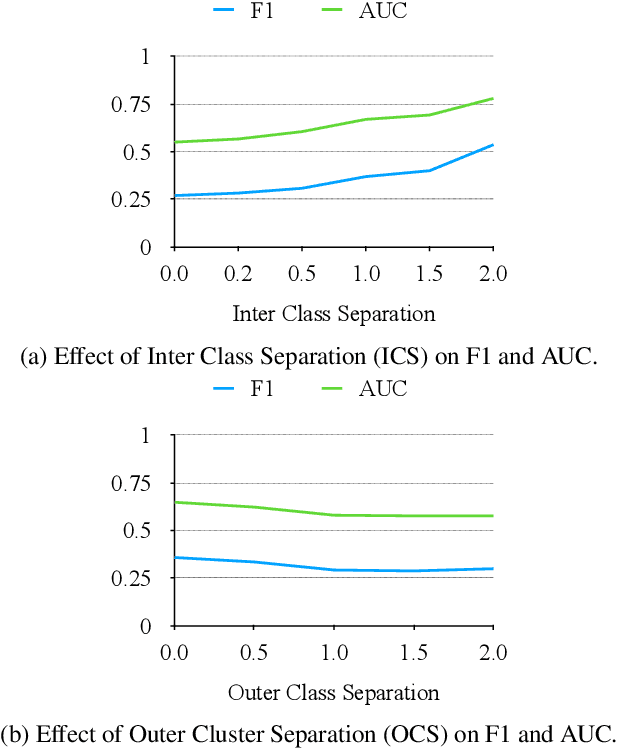
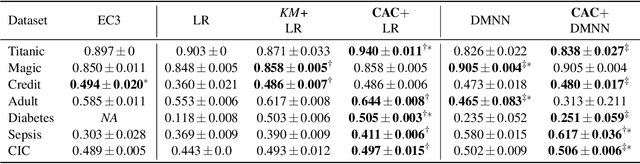
In data containing heterogeneous subpopulations, classification performance benefits from incorporating the knowledge of cluster structure in the classifier. Previous methods for such combined clustering and classification either are classifier-specific and not generic or independently perform clustering and classifier training, which may not form clusters that can potentially benefit classifier performance. The question of how to perform clustering to improve the performance of classifiers trained on the clusters has received scant attention in previous literature despite its importance in several real-world applications. In this paper, we theoretically analyze when and how clustering may help in obtaining accurate classifiers. We design a simple, efficient, and generic framework called Classification Aware Clustering (CAC), to find clusters that are well suited for being used as training datasets by classifiers for each underlying subpopulation. Our experiments on synthetic and real benchmark datasets demonstrate the efficacy of CAC over previous methods for combined clustering and classification.

Coresets for Regressions with Panel Data

This paper introduces the problem of coresets for regression problems to panel data settings. We first define coresets for several variants of regression problems with panel data and then present efficient algorithms to construct coresets of size that depend polynomially on 1/$\varepsilon$ (where $\varepsilon$ is the error parameter) and the number of regression parameters - independent of the number of individuals in the panel data or the time units each individual is observed for. Our approach is based on the Feldman-Langberg framework in which a key step is to upper bound the "total sensitivity" that is roughly the sum of maximum influences of all individual-time pairs taken over all possible choices of regression parameters. Empirically, we assess our approach with synthetic and real-world datasets; the coreset sizes constructed using our approach are much smaller than the full dataset and coresets indeed accelerate the running time of computing the regression objective.