Using Advanced LLMs to Enhance Smaller LLMs: An Interpretable Knowledge Distillation Approach

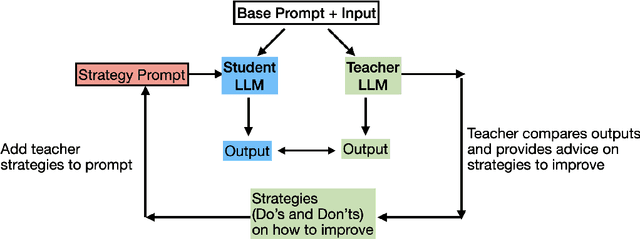
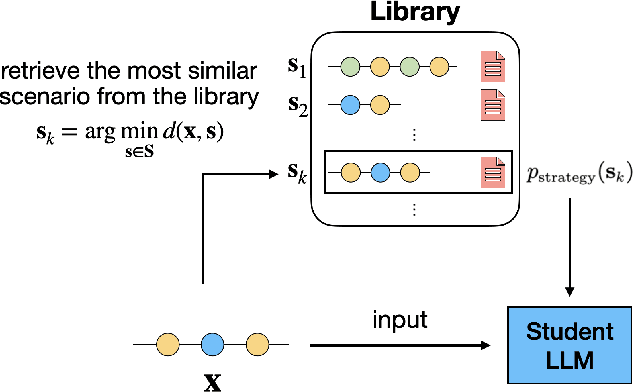
Advanced Large language models (LLMs) like GPT-4 or LlaMa 3 provide superior performance in complex human-like interactions. But they are costly, or too large for edge devices such as smartphones and harder to self-host, leading to security and privacy concerns. This paper introduces a novel interpretable knowledge distillation approach to enhance the performance of smaller, more economical LLMs that firms can self-host. We study this problem in the context of building a customer service agent aimed at achieving high customer satisfaction through goal-oriented dialogues. Unlike traditional knowledge distillation, where the "student" model learns directly from the "teacher" model's responses via fine-tuning, our interpretable "strategy" teaching approach involves the teacher providing strategies to improve the student's performance in various scenarios. This method alternates between a "scenario generation" step and a "strategies for improvement" step, creating a customized library of scenarios and optimized strategies for automated prompting. The method requires only black-box access to both student and teacher models; hence it can be used without manipulating model parameters. In our customer service application, the method improves performance, and the learned strategies are transferable to other LLMs and scenarios beyond the training set. The method's interpretabilty helps safeguard against potential harms through human audit.

A Theory-Based Explainable Deep Learning Architecture for Music Emotion

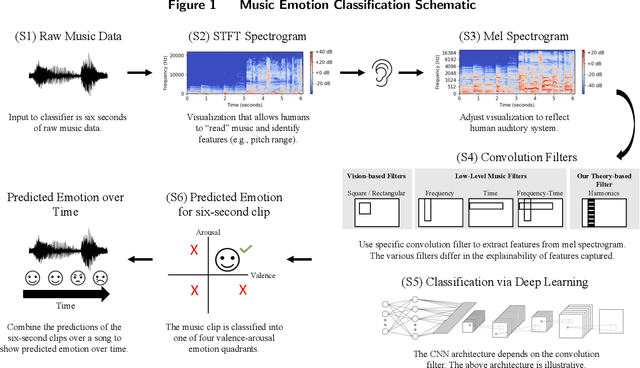
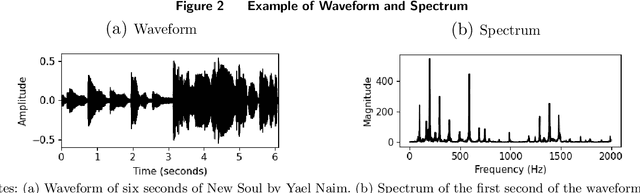
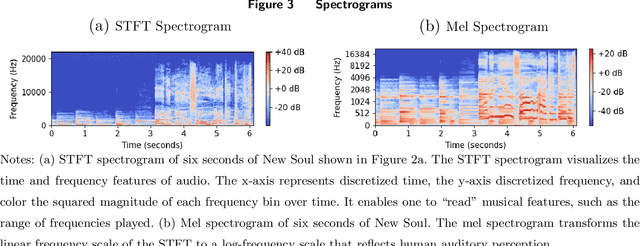
This paper paper develops a theory-based, explainable deep learning convolutional neural network (CNN) classifier to predict the time-varying emotional response to music. We design novel CNN filters that leverage the frequency harmonics structure from acoustic physics known to impact the perception of musical features. Our theory-based model is more parsimonious, but provides comparable predictive performance to atheoretical deep learning models, while performing better than models using handcrafted features. Our model can be complemented with handcrafted features, but the performance improvement is marginal. Importantly, the harmonics-based structure placed on the CNN filters provides better explainability for how the model predicts emotional response (valence and arousal), because emotion is closely related to consonance--a perceptual feature defined by the alignment of harmonics. Finally, we illustrate the utility of our model with an application involving digital advertising. Motivated by YouTube mid-roll ads, we conduct a lab experiment in which we exogenously insert ads at different times within videos. We find that ads placed in emotionally similar contexts increase ad engagement (lower skip rates, higher brand recall rates). Ad insertion based on emotional similarity metrics predicted by our theory-based, explainable model produces comparable or better engagement relative to atheoretical models.

Coresets for Time Series Clustering

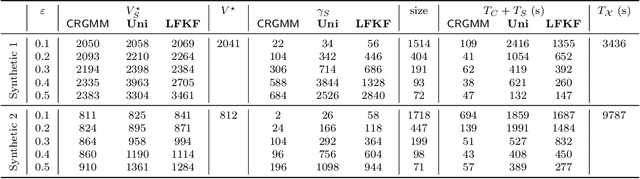
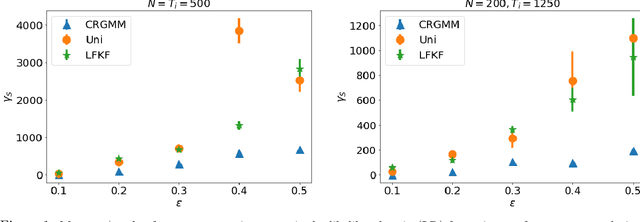
We study the problem of constructing coresets for clustering problems with time series data. This problem has gained importance across many fields including biology, medicine, and economics due to the proliferation of sensors facilitating real-time measurement and rapid drop in storage costs. In particular, we consider the setting where the time series data on $N$ entities is generated from a Gaussian mixture model with autocorrelations over $k$ clusters in $\mathbb{R}^d$. Our main contribution is an algorithm to construct coresets for the maximum likelihood objective for this mixture model. Our algorithm is efficient, and under a mild boundedness assumption on the covariance matrices of the underlying Gaussians, the size of the coreset is independent of the number of entities $N$ and the number of observations for each entity, and depends only polynomially on $k$, $d$ and $1/\varepsilon$, where $\varepsilon$ is the error parameter. We empirically assess the performance of our coreset with synthetic data.

Coresets for Regressions with Panel Data

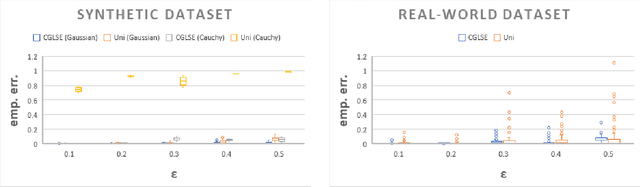
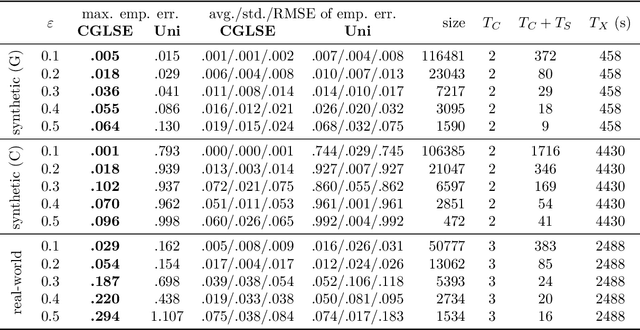
This paper introduces the problem of coresets for regression problems to panel data settings. We first define coresets for several variants of regression problems with panel data and then present efficient algorithms to construct coresets of size that depend polynomially on 1/$\varepsilon$ (where $\varepsilon$ is the error parameter) and the number of regression parameters - independent of the number of individuals in the panel data or the time units each individual is observed for. Our approach is based on the Feldman-Langberg framework in which a key step is to upper bound the "total sensitivity" that is roughly the sum of maximum influences of all individual-time pairs taken over all possible choices of regression parameters. Empirically, we assess our approach with synthetic and real-world datasets; the coreset sizes constructed using our approach are much smaller than the full dataset and coresets indeed accelerate the running time of computing the regression objective.