A Provable Expressiveness Hierarchy in Hybrid Linear-Full Attention

Transformers serve as the foundation of most modern large language models. To mitigate the quadratic complexity of standard full attention, various efficient attention mechanisms, such as linear and hybrid attention, have been developed. A fundamental gap remains: their expressive power relative to full attention lacks a rigorous theoretical characterization. In this work, we theoretically characterize the performance differences among these attention mechanisms. Our theory applies to all linear attention variants that can be formulated as a recurrence, including Mamba, DeltaNet, etc. Specifically, we establish an expressiveness hierarchy: for the sequential function composition-a multi-step reasoning task that must occur within a model's forward pass, an ($L+1$)-layer full attention network is sufficient, whereas any hybrid network interleaving $L-1$ layers of full attention with a substantially larger number ($2^{3L^2}$) of linear attention layers cannot solve it. This result demonstrates a clear separation in expressive power between the two types of attention. Our work provides the first provable separation between hybrid attention and standard full attention, offering a theoretical perspective for understanding the fundamental capabilities and limitations of different attention mechanisms.

BAPS: A Fine-Grained Low-Precision Scheme for Softmax in Attention via Block-Aware Precision reScaling

As the performance gains from accelerating quantized matrix multiplication plateau, the softmax operation becomes the critical bottleneck in Transformer inference. This bottleneck stems from two hardware limitations: (1) limited data bandwidth between matrix and vector compute cores, and (2) the significant area cost of high-precision (FP32/16) exponentiation units (EXP2). To address these issues, we introduce a novel low-precision workflow that employs a specific 8-bit floating-point format (HiF8) and block-aware precision rescaling for softmax. Crucially, our algorithmic innovations make low-precision softmax feasible without the significant model accuracy loss that hampers direct low-precision approaches. Specifically, our design (i) halves the required data movement bandwidth by enabling matrix multiplication outputs constrained to 8-bit, and (ii) substantially reduces the EXP2 unit area by computing exponentiations in low (8-bit) precision. Extensive evaluation on language models and multi-modal models confirms the validity of our method. By alleviating the vector computation bottleneck, our work paves the way for doubling end-to-end inference throughput without increasing chip area, and offers a concrete co-design path for future low-precision hardware and software.

On the Ability of LLMs to Handle Character-Level Perturbations: How Well and How?

This work investigates the resilience of contemporary LLMs against frequent and structured character-level perturbations, specifically through the insertion of noisy characters after each input character. We introduce \nameshort{}, a practical method that inserts invisible Unicode control characters into text to discourage LLM misuse in scenarios such as online exam systems. Surprisingly, despite strong obfuscation that fragments tokenization and reduces the signal-to-noise ratio significantly, many LLMs still maintain notable performance. Through comprehensive evaluation across model-, problem-, and noise-related configurations, we examine the extent and mechanisms of this robustness, exploring both the handling of character-level tokenization and \textit{implicit} versus \textit{explicit} denoising mechanism hypotheses of character-level noises. We hope our findings on the low-level robustness of LLMs will shed light on the risks of their misuse and on the reliability of deploying LLMs across diverse applications.

Tight Regret Bounds for Fixed-Price Bilateral Trade

We examine fixed-price mechanisms in bilateral trade through the lens of regret minimization. Our main results are twofold. (i) For independent values, a near-optimal $\widetilde{\Theta}(T^{2/3})$ tight bound for $\textsf{Global Budget Balance}$ fixed-price mechanisms with two-bit/one-bit feedback. (ii) For correlated/adversarial values, a near-optimal $\Omega(T^{3/4})$ lower bound for $\textsf{Global Budget Balance}$ fixed-price mechanisms with two-bit/one-bit feedback, which improves the best known $\Omega(T^{5/7})$ lower bound obtained in the work \cite{BCCF24} and, up to polylogarithmic factors, matches the $\widetilde{\mathcal{O}}(T^{3 / 4})$ upper bound obtained in the same work. Our work in combination with the previous works \cite{CCCFL24mor, CCCFL24jmlr, AFF24, BCCF24} (essentially) gives a thorough understanding of regret minimization for fixed-price bilateral trade. En route, we have developed two technical ingredients that might be of independent interest: (i) A novel algorithmic paradigm, called $\textit{{fractal elimination}}$, to address one-bit feedback and independent values. (ii) A new $\textit{lower-bound construction}$ with novel proof techniques, to address the $\textsf{Global Budget Balance}$ constraint and correlated values.

A Hierarchical Destroy and Repair Approach for Solving Very Large-Scale Travelling Salesman Problem

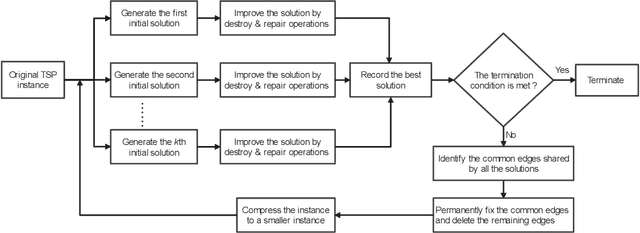
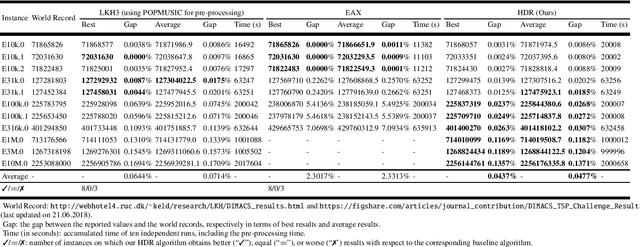
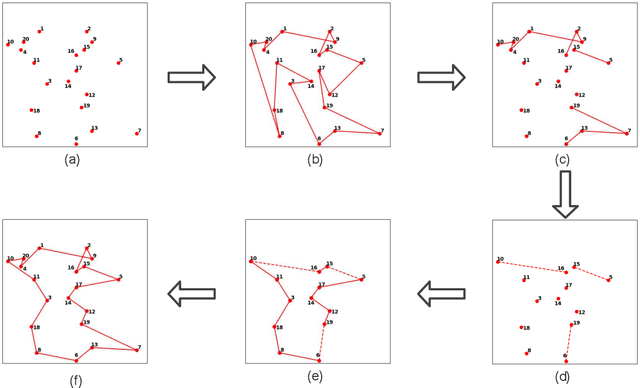
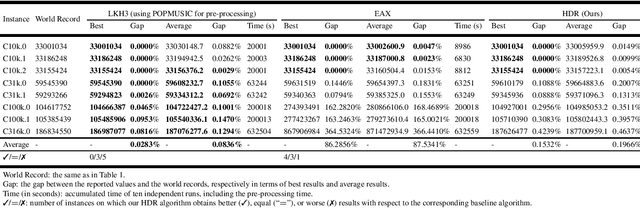
For prohibitively large-scale Travelling Salesman Problems (TSPs), existing algorithms face big challenges in terms of both computational efficiency and solution quality. To address this issue, we propose a hierarchical destroy-and-repair (HDR) approach, which attempts to improve an initial solution by applying a series of carefully designed destroy-and-repair operations. A key innovative concept is the hierarchical search framework, which recursively fixes partial edges and compresses the input instance into a small-scale TSP under some equivalence guarantee. This neat search framework is able to deliver highly competitive solutions within a reasonable time. Fair comparisons based on nineteen famous large-scale instances (with 10,000 to 10,000,000 cities) show that HDR is highly competitive against existing state-of-the-art TSP algorithms, in terms of both efficiency and solution quality. Notably, on two large instances with 3,162,278 and 10,000,000 cities, HDR breaks the world records (i.e., best-known results regardless of computation time), which were previously achieved by LKH and its variants, while HDR is completely independent of LKH. Finally, ablation studies are performed to certify the importance and validity of the hierarchical search framework.

Variance-Dependent Best Arm Identification

We study the problem of identifying the best arm in a stochastic multi-armed bandit game. Given a set of $n$ arms indexed from $1$ to $n$, each arm $i$ is associated with an unknown reward distribution supported on $[0,1]$ with mean $\theta_i$ and variance $\sigma_i^2$. Assume $\theta_1 > \theta_2 \geq \cdots \geq\theta_n$. We propose an adaptive algorithm which explores the gaps and variances of the rewards of the arms and makes future decisions based on the gathered information using a novel approach called \textit{grouped median elimination}. The proposed algorithm guarantees to output the best arm with probability $(1-\delta)$ and uses at most $O \left(\sum_{i = 1}^n \left(\frac{\sigma_i^2}{\Delta_i^2} + \frac{1}{\Delta_i}\right)(\ln \delta^{-1} + \ln \ln \Delta_i^{-1})\right)$ samples, where $\Delta_i$ ($i \geq 2$) denotes the reward gap between arm $i$ and the best arm and we define $\Delta_1 = \Delta_2$. This achieves a significant advantage over the variance-independent algorithms in some favorable scenarios and is the first result that removes the extra $\ln n$ factor on the best arm compared with the state-of-the-art. We further show that $\Omega \left( \sum_{i = 1}^n \left( \frac{\sigma_i^2}{\Delta_i^2} + \frac{1}{\Delta_i} \right) \ln \delta^{-1} \right)$ samples are necessary for an algorithm to achieve the same goal, thereby illustrating that our algorithm is optimal up to doubly logarithmic terms.

Combinatorial Multi-Armed Bandit with General Reward Functions

In this paper, we study the stochastic combinatorial multi-armed bandit (CMAB) framework that allows a general nonlinear reward function, whose expected value may not depend only on the means of the input random variables but possibly on the entire distributions of these variables. Our framework enables a much larger class of reward functions such as the $\max()$ function and nonlinear utility functions. Existing techniques relying on accurate estimations of the means of random variables, such as the upper confidence bound (UCB) technique, do not work directly on these functions. We propose a new algorithm called stochastically dominant confidence bound (SDCB), which estimates the distributions of underlying random variables and their stochastically dominant confidence bounds. We prove that SDCB can achieve $O(\log{T})$ distribution-dependent regret and $\tilde{O}(\sqrt{T})$ distribution-independent regret, where $T$ is the time horizon. We apply our results to the $K$-MAX problem and expected utility maximization problems. In particular, for $K$-MAX, we provide the first polynomial-time approximation scheme (PTAS) for its offline problem, and give the first $\tilde{O}(\sqrt T)$ bound on the $(1-\epsilon)$-approximation regret of its online problem, for any $\epsilon>0$.