On the Problem of Best Arm Retention

This paper presents a comprehensive study on the problem of Best Arm Retention (BAR), which has recently found applications in streaming algorithms for multi-armed bandits. In the BAR problem, the goal is to retain $m$ arms with the best arm included from $n$ after some trials, in stochastic multi-armed bandit settings. We first investigate pure exploration for the BAR problem under different criteria, and then minimize the regret with specific constraints, in the context of further exploration in streaming algorithms. - We begin by revisiting the lower bound for the $(\varepsilon,\delta)$-PAC algorithm for Best Arm Identification (BAI) and adapt the classical KL-divergence argument to derive optimal bounds for $(\varepsilon,\delta)$-PAC algorithms for BAR. - We further study another variant of the problem, called $r$-BAR, which requires the expected gap between the best arm and the optimal arm retained is less than $r$. We prove tight sample complexity for the problem. - We explore the regret minimization problem for $r$-BAR and develop algorithm beyond pure exploration. We conclude with a conjecture on the optimal regret in this setting.

Tight Regret Bounds for Fixed-Price Bilateral Trade

We examine fixed-price mechanisms in bilateral trade through the lens of regret minimization. Our main results are twofold. (i) For independent values, a near-optimal $\widetilde{\Theta}(T^{2/3})$ tight bound for $\textsf{Global Budget Balance}$ fixed-price mechanisms with two-bit/one-bit feedback. (ii) For correlated/adversarial values, a near-optimal $\Omega(T^{3/4})$ lower bound for $\textsf{Global Budget Balance}$ fixed-price mechanisms with two-bit/one-bit feedback, which improves the best known $\Omega(T^{5/7})$ lower bound obtained in the work \cite{BCCF24} and, up to polylogarithmic factors, matches the $\widetilde{\mathcal{O}}(T^{3 / 4})$ upper bound obtained in the same work. Our work in combination with the previous works \cite{CCCFL24mor, CCCFL24jmlr, AFF24, BCCF24} (essentially) gives a thorough understanding of regret minimization for fixed-price bilateral trade. En route, we have developed two technical ingredients that might be of independent interest: (i) A novel algorithmic paradigm, called $\textit{{fractal elimination}}$, to address one-bit feedback and independent values. (ii) A new $\textit{lower-bound construction}$ with novel proof techniques, to address the $\textsf{Global Budget Balance}$ constraint and correlated values.

Tight Gap-Dependent Memory-Regret Trade-Off for Single-Pass Streaming Stochastic Multi-Armed Bandits

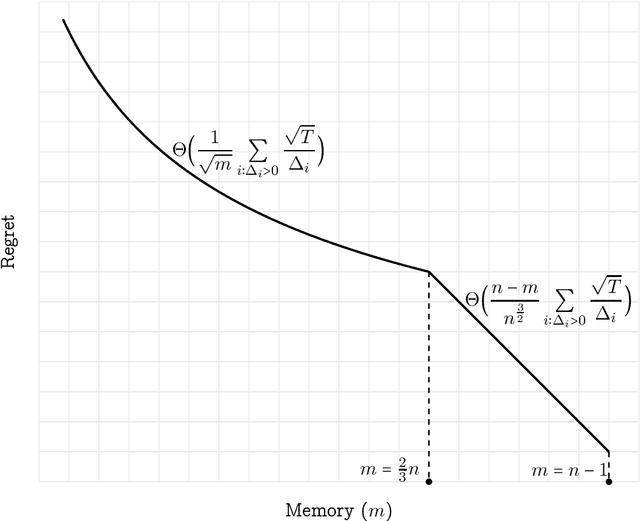
We study the problem of minimizing gap-dependent regret for single-pass streaming stochastic multi-armed bandits (MAB). In this problem, the $n$ arms are present in a stream, and at most $m<n$ arms and their statistics can be stored in the memory. We establish tight non-asymptotic regret bounds regarding all relevant parameters, including the number of arms $n$, the memory size $m$, the number of rounds $T$ and $(\Delta_i)_{i\in [n]}$ where $\Delta_i$ is the reward mean gap between the best arm and the $i$-th arm. These gaps are not known in advance by the player. Specifically, for any constant $\alpha \ge 1$, we present two algorithms: one applicable for $m\ge \frac{2}{3}n$ with regret at most $O_\alpha\Big(\frac{(n-m)T^{\frac{1}{\alpha + 1}}}{n^{1 + {\frac{1}{\alpha + 1}}}}\displaystyle\sum_{i:\Delta_i > 0}\Delta_i^{1 - 2\alpha}\Big)$ and another applicable for $m<\frac{2}{3}n$ with regret at most $O_\alpha\Big(\frac{T^{\frac{1}{\alpha+1}}}{m^{\frac{1}{\alpha+1}}}\displaystyle\sum_{i:\Delta_i > 0}\Delta_i^{1 - 2\alpha}\Big)$. We also prove matching lower bounds for both cases by showing that for any constant $\alpha\ge 1$ and any $m\leq k < n$, there exists a set of hard instances on which the regret of any algorithm is $\Omega_\alpha\Big(\frac{(k-m+1) T^{\frac{1}{\alpha+1}}}{k^{1 + \frac{1}{\alpha+1}}} \sum_{i:\Delta_i > 0}\Delta_i^{1-2\alpha}\Big)$. This is the first tight gap-dependent regret bound for streaming MAB. Prior to our work, an $O\Big(\sum_{i\colon\Delta>0} \frac{\sqrt{T}\log T}{\Delta_i}\Big)$ upper bound for the special case of $\alpha=1$ and $m=O(1)$ was established by Agarwal, Khanna and Patil (COLT'22). In contrast, our results provide the correct order of regret as $\Theta\Big(\frac{1}{\sqrt{m}}\sum_{i\colon\Delta>0}\frac{\sqrt{T}}{\Delta_i}\Big)$.

On the query complexity of sampling from non-log-concave distributions

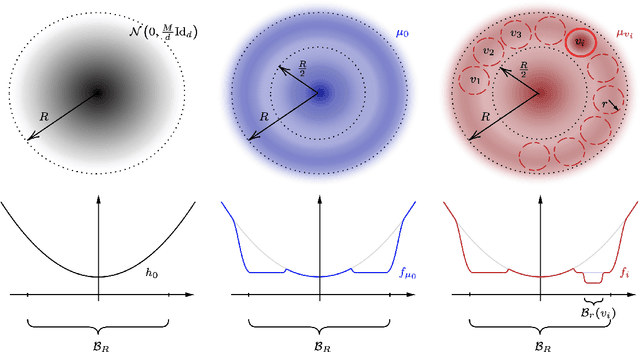
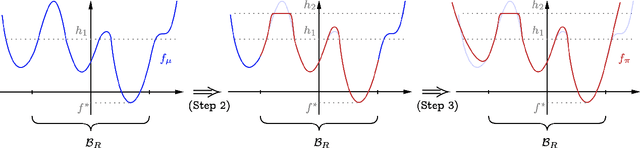
We study the problem of sampling from a $d$-dimensional distribution with density $p(x)\propto e^{-f(x)}$, which does not necessarily satisfy good isoperimetric conditions. Specifically, we show that for any $L,M$ satisfying $LM\ge d\ge 5$, $\epsilon\in \left\{0,\frac{1}{32}\right\}$, and any algorithm with query accesses to the value of $f(x)$ and $\nabla f(x)$, there exists an $L$-log-smooth distribution with second moment at most $M$ such that the algorithm requires $\left\{\frac{LM}{d\epsilon}\right\}^{\Omega(d)}$ queries to compute a sample whose distribution is within $\epsilon$ in total variation distance to the target distribution. We complement the lower bound with an algorithm requiring $\left\{\frac{LM}{d\epsilon}\right\}^{\mathcal O(d)}$ queries, thereby characterizing the tight (up to the constant in the exponent) query complexity for sampling from the family of non-log-concave distributions. Our results are in sharp contrast with the recent work of Huang et al. (COLT'24), where an algorithm with quasi-polynomial query complexity was proposed for sampling from a non-log-concave distribution when $M=\mathtt{poly}(d)$. Their algorithm works under the stronger condition that all distributions along the trajectory of the Ornstein-Uhlenbeck process, starting from the target distribution, are $\mathcal O(1)$-log-smooth. We investigate this condition and prove that it is strictly stronger than requiring the target distribution to be $\mathcal O(1)$-log-smooth. Additionally, we study this condition in the context of mixtures of Gaussians. Finally, we place our results within the broader theme of ``sampling versus optimization'', as studied in Ma et al. (PNAS'19). We show that for a wide range of parameters, sampling is strictly easier than optimization by a super-exponential factor in the dimension $d$.

Dynamical causality under invisible confounders

Causality inference is prone to spurious causal interactions, due to the substantial confounders in a complex system. While many existing methods based on the statistical methods or dynamical methods attempt to address misidentification challenges, there remains a notable lack of effective methods to infer causality, in particular in the presence of invisible/unobservable confounders. As a result, accurately inferring causation with invisible confounders remains a largely unexplored and outstanding issue in data science and AI fields. In this work, we propose a method to overcome such challenges to infer dynamical causality under invisible confounders (CIC method) and further reconstruct the invisible confounders from time-series data by developing an orthogonal decomposition theorem in a delay embedding space. The core of our CIC method lies in its ability to decompose the observed variables not in their original space but in their delay embedding space into the common and private subspaces respectively, thereby quantifying causality between those variables both theoretically and computationally. This theoretical foundation ensures the causal detection for any high-dimensional system even with only two observed variables under many invisible confounders, which is actually a long-standing problem in the field. In addition to the invisible confounder problem, such a decomposition actually makes the intertwined variables separable in the embedding space, thus also solving the non-separability problem of causal inference. Extensive validation of the CIC method is carried out using various real datasets, and the experimental results demonstrates its effectiveness to reconstruct real biological networks even with unobserved confounders.

Understanding Memory-Regret Trade-Off for Streaming Stochastic Multi-Armed Bandits

We study the stochastic multi-armed bandit problem in the $P$-pass streaming model. In this problem, the $n$ arms are present in a stream and at most $m<n$ arms and their statistics can be stored in the memory. We give a complete characterization of the optimal regret in terms of $m, n$ and $P$. Specifically, we design an algorithm with $\tilde O\left((n-m)^{1+\frac{2^{P}-2}{2^{P+1}-1}} n^{\frac{2-2^{P+1}}{2^{P+1}-1}} T^{\frac{2^P}{2^{P+1}-1}}\right)$ regret and complement it with an $\tilde \Omega\left((n-m)^{1+\frac{2^{P}-2}{2^{P+1}-1}} n^{\frac{2-2^{P+1}}{2^{P+1}-1}} T^{\frac{2^P}{2^{P+1}-1}}\right)$ lower bound when the number of rounds $T$ is sufficiently large. Our results are tight up to a logarithmic factor in $n$ and $P$.

On Interpolating Experts and Multi-Armed Bandits

Learning with expert advice and multi-armed bandit are two classic online decision problems which differ on how the information is observed in each round of the game. We study a family of problems interpolating the two. For a vector $\mathbf{m}=(m_1,\dots,m_K)\in \mathbb{N}^K$, an instance of $\mathbf{m}$-MAB indicates that the arms are partitioned into $K$ groups and the $i$-th group contains $m_i$ arms. Once an arm is pulled, the losses of all arms in the same group are observed. We prove tight minimax regret bounds for $\mathbf{m}$-MAB and design an optimal PAC algorithm for its pure exploration version, $\mathbf{m}$-BAI, where the goal is to identify the arm with minimum loss with as few rounds as possible. We show that the minimax regret of $\mathbf{m}$-MAB is $\Theta\left(\sqrt{T\sum_{k=1}^K\log (m_k+1)}\right)$ and the minimum number of pulls for an $(\epsilon,0.05)$-PAC algorithm of $\mathbf{m}$-BAI is $\Theta\left(\frac{1}{\epsilon^2}\cdot \sum_{k=1}^K\log (m_k+1)\right)$. Both our upper bounds and lower bounds for $\mathbf{m}$-MAB can be extended to a more general setting, namely the bandit with graph feedback, in terms of the clique cover and related graph parameters. As consequences, we obtained tight minimax regret bounds for several families of feedback graphs.

Improved Algorithms for Bandit with Graph Feedback via Regret Decomposition

The problem of bandit with graph feedback generalizes both the multi-armed bandit (MAB) problem and the learning with expert advice problem by encoding in a directed graph how the loss vector can be observed in each round of the game. The mini-max regret is closely related to the structure of the feedback graph and their connection is far from being fully understood. We propose a new algorithmic framework for the problem based on a partition of the feedback graph. Our analysis reveals the interplay between various parts of the graph by decomposing the regret to the sum of the regret caused by small parts and the regret caused by their interaction. As a result, our algorithm can be viewed as an interpolation and generalization of the optimal algorithms for MAB and learning with expert advice. Our framework unifies previous algorithms for both strongly observable graphs and weakly observable graphs, resulting in improved and optimal regret bounds on a wide range of graph families including graphs of bounded degree and strongly observable graphs with a few corrupted arms.

Information-theoretic Classification Accuracy: A Criterion that Guides Data-driven Combination of Ambiguous Outcome Labels in Multi-class Classification

Outcome labeling ambiguity and subjectivity are ubiquitous in real-world datasets. While practitioners commonly combine ambiguous outcome labels in an ad hoc way to improve the accuracy of multi-class classification, there lacks a principled approach to guide label combination by any optimality criterion. To address this problem, we propose the information-theoretic classification accuracy (ITCA), a criterion of outcome "information" conditional on outcome prediction, to guide practitioners on how to combine ambiguous outcome labels. ITCA indicates a balance in the trade-off between prediction accuracy (how well do predicted labels agree with actual labels) and prediction resolution (how many labels are predictable). To find the optimal label combination indicated by ITCA, we develop two search strategies: greedy search and breadth-first search. Notably, ITCA and the two search strategies are adaptive to all machine-learning classification algorithms. Coupled with a classification algorithm and a search strategy, ITCA has two uses: to improve prediction accuracy and to identify ambiguous labels. We first verify that ITCA achieves high accuracy with both search strategies in finding the correct label combinations on synthetic and real data. Then we demonstrate the effectiveness of ITCA in diverse applications including medical prognosis, cancer survival prediction, user demographics prediction, and cell type classification.

Understanding Bandits with Graph Feedback

The bandit problem with graph feedback, proposed in [Mannor and Shamir, NeurIPS 2011], is modeled by a directed graph $G=(V,E)$ where $V$ is the collection of bandit arms, and once an arm is triggered, all its incident arms are observed. A fundamental question is how the structure of the graph affects the min-max regret. We propose the notions of the fractional weak domination number $\delta^*$ and the $k$-packing independence number capturing upper bound and lower bound for the regret respectively. We show that the two notions are inherently connected via aligning them with the linear program of the weakly dominating set and its dual -- the fractional vertex packing set respectively. Based on this connection, we utilize the strong duality theorem to prove a general regret upper bound $O\left(\left( \delta^*\log |V|\right)^{\frac{1}{3}}T^{\frac{2}{3}}\right)$ and a lower bound $\Omega\left(\left(\delta^*/\alpha\right)^{\frac{1}{3}}T^{\frac{2}{3}}\right)$ where $\alpha$ is the integrality gap of the dual linear program. Therefore, our bounds are tight up to a $\left(\log |V|\right)^{\frac{1}{3}}$ factor on graphs with bounded integrality gap for the vertex packing problem including trees and graphs with bounded degree. Moreover, we show that for several special families of graphs, we can get rid of the $\left(\log |V|\right)^{\frac{1}{3}}$ factor and establish optimal regret.