Brain-inspired Chaotic Graph Backpropagation for Large-scale Combinatorial Optimization

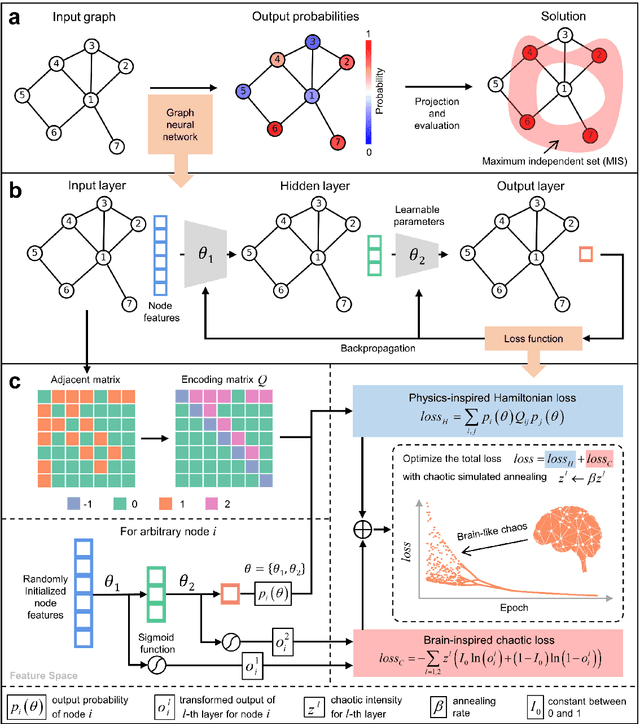
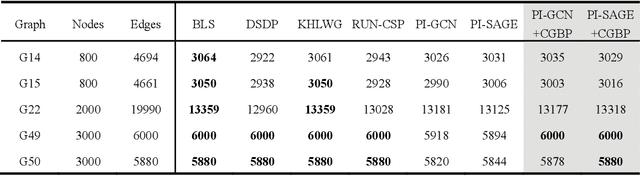
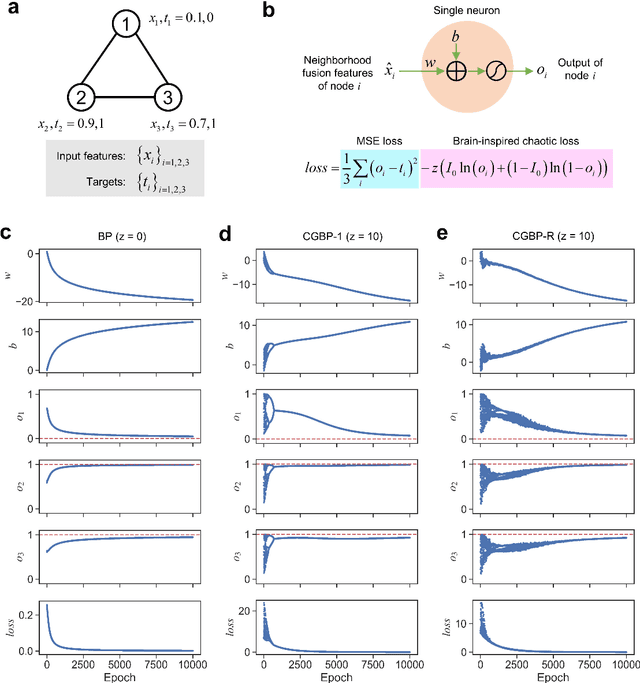
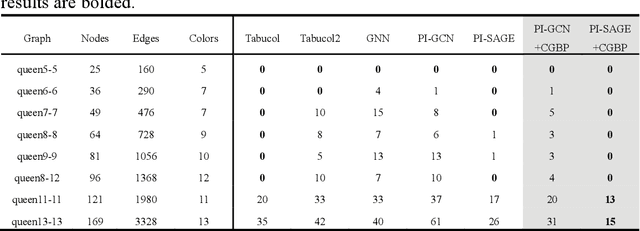
Graph neural networks (GNNs) with unsupervised learning can solve large-scale combinatorial optimization problems (COPs) with efficient time complexity, making them versatile for various applications. However, since this method maps the combinatorial optimization problem to the training process of a graph neural network, and the current mainstream backpropagation-based training algorithms are prone to fall into local minima, the optimization performance is still inferior to the current state-of-the-art (SOTA) COP methods. To address this issue, inspired by possibly chaotic dynamics of real brain learning, we introduce a chaotic training algorithm, i.e. chaotic graph backpropagation (CGBP), which introduces a local loss function in GNN that makes the training process not only chaotic but also highly efficient. Different from existing methods, we show that the global ergodicity and pseudo-randomness of such chaotic dynamics enable CGBP to learn each optimal GNN effectively and globally, thus solving the COP efficiently. We have applied CGBP to solve various COPs, such as the maximum independent set, maximum cut, and graph coloring. Results on several large-scale benchmark datasets showcase that CGBP can outperform not only existing GNN algorithms but also SOTA methods. In addition to solving large-scale COPs, CGBP as a universal learning algorithm for GNNs, i.e. as a plug-in unit, can be easily integrated into any existing method for improving the performance.

Dynamical causality under invisible confounders

Causality inference is prone to spurious causal interactions, due to the substantial confounders in a complex system. While many existing methods based on the statistical methods or dynamical methods attempt to address misidentification challenges, there remains a notable lack of effective methods to infer causality, in particular in the presence of invisible/unobservable confounders. As a result, accurately inferring causation with invisible confounders remains a largely unexplored and outstanding issue in data science and AI fields. In this work, we propose a method to overcome such challenges to infer dynamical causality under invisible confounders (CIC method) and further reconstruct the invisible confounders from time-series data by developing an orthogonal decomposition theorem in a delay embedding space. The core of our CIC method lies in its ability to decompose the observed variables not in their original space but in their delay embedding space into the common and private subspaces respectively, thereby quantifying causality between those variables both theoretically and computationally. This theoretical foundation ensures the causal detection for any high-dimensional system even with only two observed variables under many invisible confounders, which is actually a long-standing problem in the field. In addition to the invisible confounder problem, such a decomposition actually makes the intertwined variables separable in the embedding space, thus also solving the non-separability problem of causal inference. Extensive validation of the CIC method is carried out using various real datasets, and the experimental results demonstrates its effectiveness to reconstruct real biological networks even with unobserved confounders.

Deciphering interventional dynamical causality from non-intervention systems

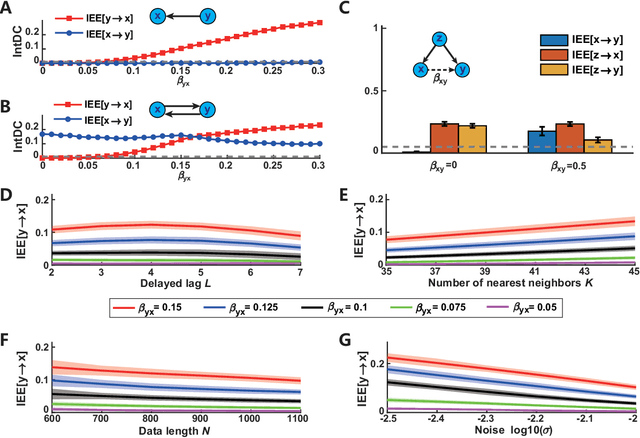
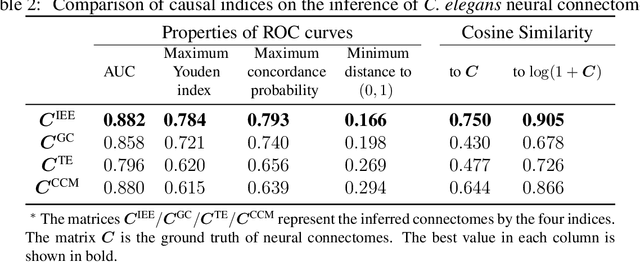
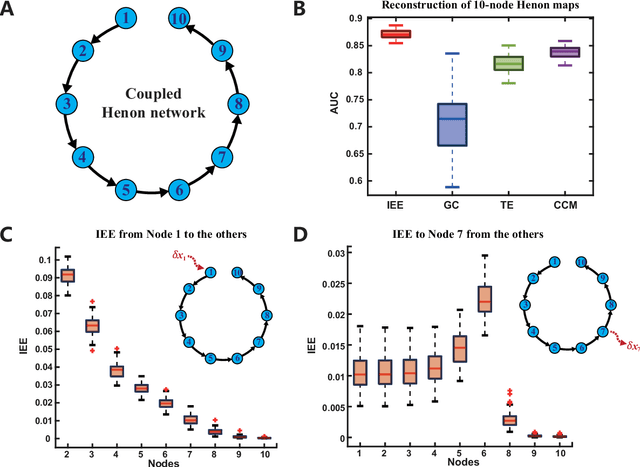
Detecting and quantifying causality is a focal topic in the fields of science, engineering, and interdisciplinary studies. However, causal studies on non-intervention systems attract much attention but remain extremely challenging. To address this challenge, we propose a framework named Interventional Dynamical Causality (IntDC) for such non-intervention systems, along with its computational criterion, Interventional Embedding Entropy (IEE), to quantify causality. The IEE criterion theoretically and numerically enables the deciphering of IntDC solely from observational (non-interventional) time-series data, without requiring any knowledge of dynamical models or real interventions in the considered system. Demonstrations of performance showed the accuracy and robustness of IEE on benchmark simulated systems as well as real-world systems, including the neural connectomes of C. elegans, COVID-19 transmission networks in Japan, and regulatory networks surrounding key circadian genes.

Time Series Prediction by Multi-task GPR with Spatiotemporal Information Transformation

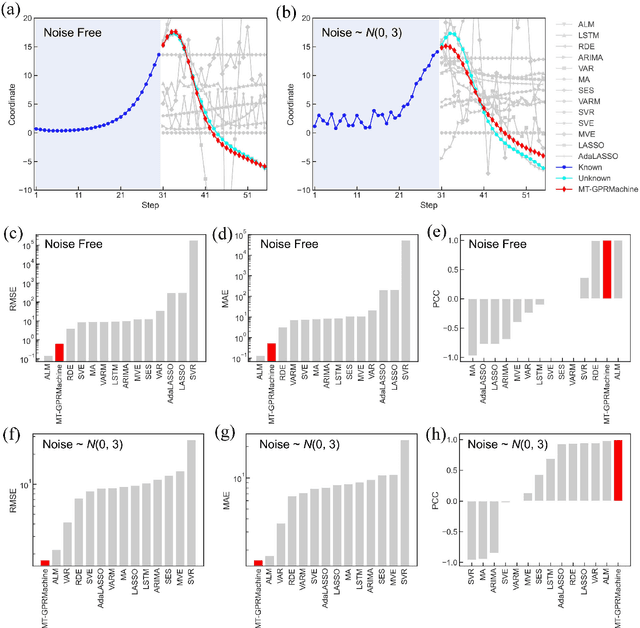
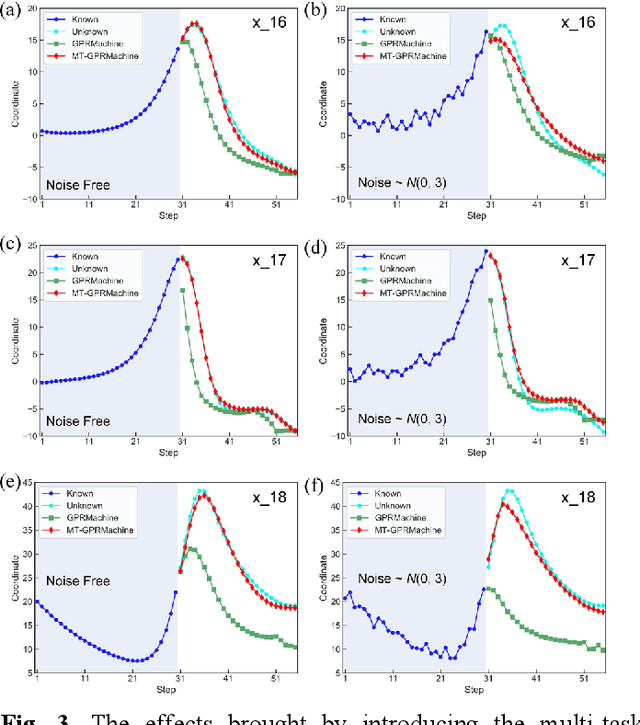
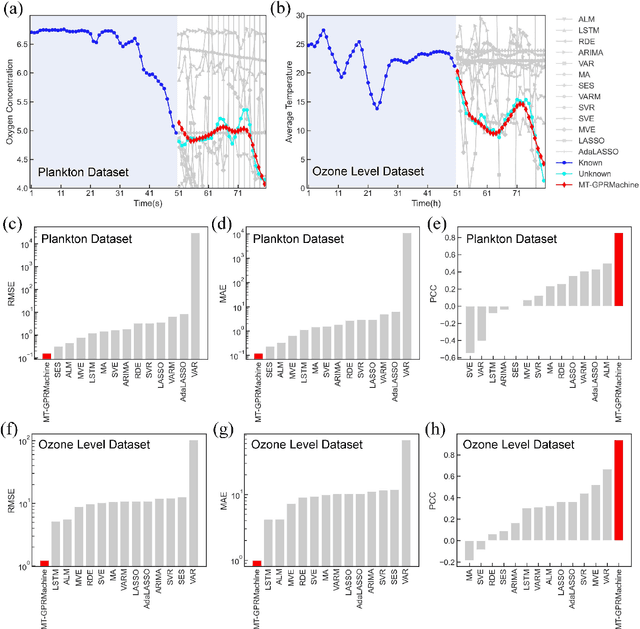
Making an accurate prediction of an unknown system only from a short-term time series is difficult due to the lack of sufficient information, especially in a multi-step-ahead manner. However, a high-dimensional short-term time series contains rich dynamical information, and also becomes increasingly available in many fields. In this work, by exploiting spatiotemporal information (STI) transformation scheme that transforms such high-dimensional/spatial information to temporal information, we developed a new method called MT-GPRMachine to achieve accurate prediction from a short-term time series. Specifically, we first construct a specific multi-task GPR which is multiple linked STI mappings to transform high dimensional/spatial information into temporal/dynamical information of any given target variable, and then makes multi step-ahead prediction of the target variable by solving those STI mappings. The multi-step-ahead prediction results on various synthetic and real-world datasets clearly validated that MT-GPRMachine outperformed other existing approaches.

Spatiotemporal convolutional network for time-series prediction and causal inference

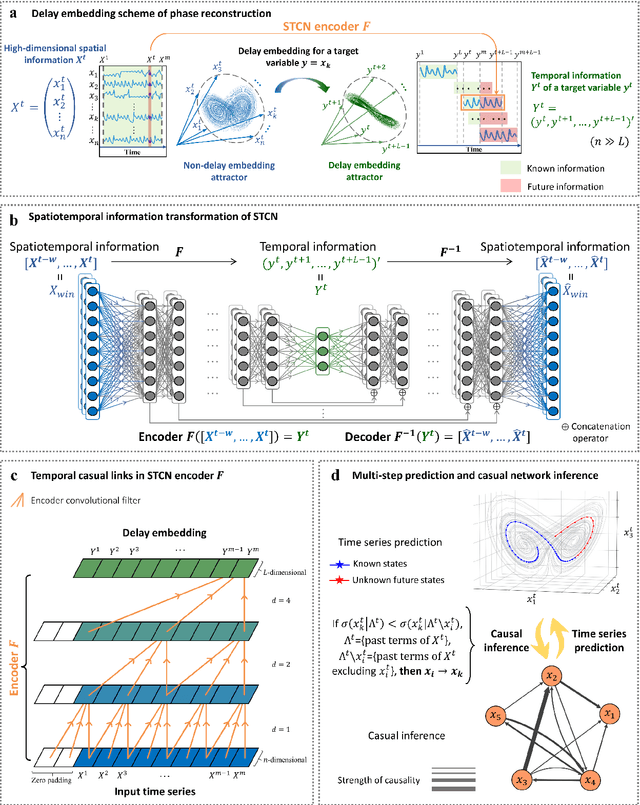
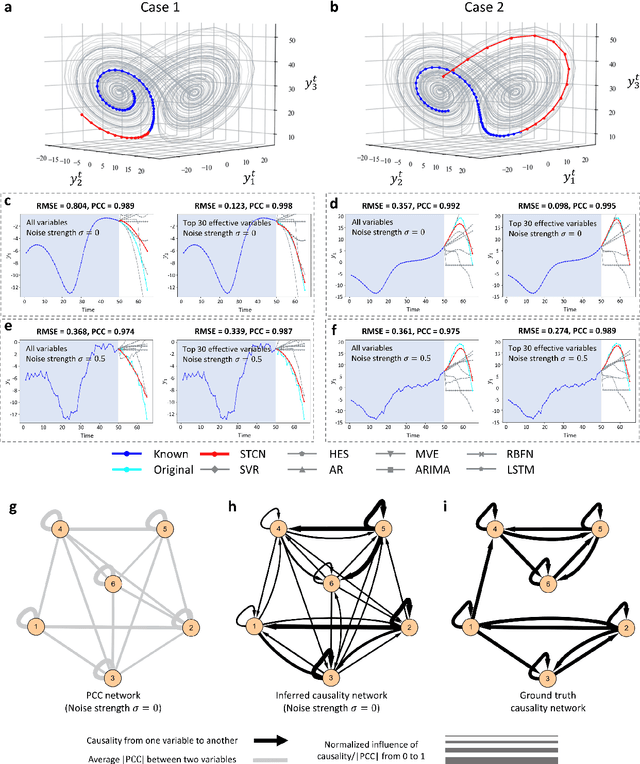
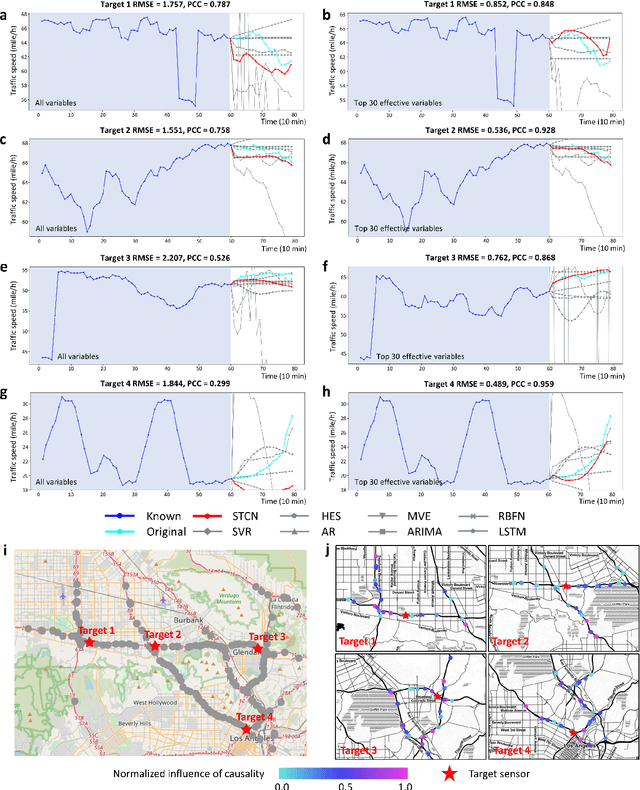
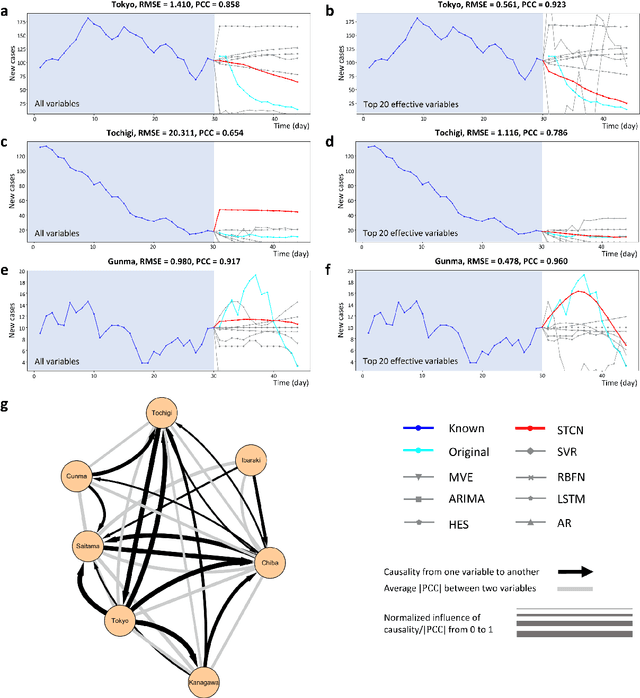
Making predictions in a robust way is not easy for nonlinear systems. In this work, a neural network computing framework, i.e., a spatiotemporal convolutional network (STCN), was developed to efficiently and accurately render a multistep-ahead prediction of a time series by employing a spatial-temporal information (STI) transformation. The STCN combines the advantages of both the temporal convolutional network (TCN) and the STI equation, which maps the high-dimensional/spatial data to the future temporal values of a target variable, thus naturally providing the prediction of the target variable. From the observed variables, the STCN also infers the causal factors of the target variable in the sense of Granger causality, which are in turn selected as effective spatial information to improve the prediction robustness. The STCN was successfully applied to both benchmark systems and real-world datasets, all of which show superior and robust performance in multistep-ahead prediction, even when the data were perturbed by noise. From both theoretical and computational viewpoints, the STCN has great potential in practical applications in artificial intelligence (AI) or machine learning fields as a model-free method based only on the observed data, and also opens a new way to explore the observed high-dimensional data in a dynamical manner for machine learning.