Utilizing Causal Network Markers to Identify Tipping Points ahead of Critical Transition

Early-warning signals of delicate design are always used to predict critical transitions in complex systems, which makes it possible to render the systems far away from the catastrophic state by introducing timely interventions. Traditional signals including the dynamical network biomarker (DNB), based on statistical properties such as variance and autocorrelation of nodal dynamics, overlook directional interactions and thus have limitations in capturing underlying mechanisms and simultaneously sustaining robustness against noise perturbations. This paper therefore introduces a framework of causal network markers (CNMs) by incorporating causality indicators, which reflect the directional influence between variables. Actually, to detect and identify the tipping points ahead of critical transition, two markers are designed: CNM-GC for linear causality and CNM-TE for non-linear causality, as well as a functional representation of different causality indicators and a clustering technique to verify the system's dominant group. Through demonstrations using benchmark models and real-world datasets of epileptic seizure, the framework of CNMs shows higher predictive power and accuracy than the traditional DNB indicator. It is believed that, due to the versatility and scalability, the CNMs are suitable for comprehensively evaluating the systems. The most possible direction for application includes the identification of tipping points in clinical disease.

Dynamical causality under invisible confounders

Causality inference is prone to spurious causal interactions, due to the substantial confounders in a complex system. While many existing methods based on the statistical methods or dynamical methods attempt to address misidentification challenges, there remains a notable lack of effective methods to infer causality, in particular in the presence of invisible/unobservable confounders. As a result, accurately inferring causation with invisible confounders remains a largely unexplored and outstanding issue in data science and AI fields. In this work, we propose a method to overcome such challenges to infer dynamical causality under invisible confounders (CIC method) and further reconstruct the invisible confounders from time-series data by developing an orthogonal decomposition theorem in a delay embedding space. The core of our CIC method lies in its ability to decompose the observed variables not in their original space but in their delay embedding space into the common and private subspaces respectively, thereby quantifying causality between those variables both theoretically and computationally. This theoretical foundation ensures the causal detection for any high-dimensional system even with only two observed variables under many invisible confounders, which is actually a long-standing problem in the field. In addition to the invisible confounder problem, such a decomposition actually makes the intertwined variables separable in the embedding space, thus also solving the non-separability problem of causal inference. Extensive validation of the CIC method is carried out using various real datasets, and the experimental results demonstrates its effectiveness to reconstruct real biological networks even with unobserved confounders.

Deciphering interventional dynamical causality from non-intervention systems

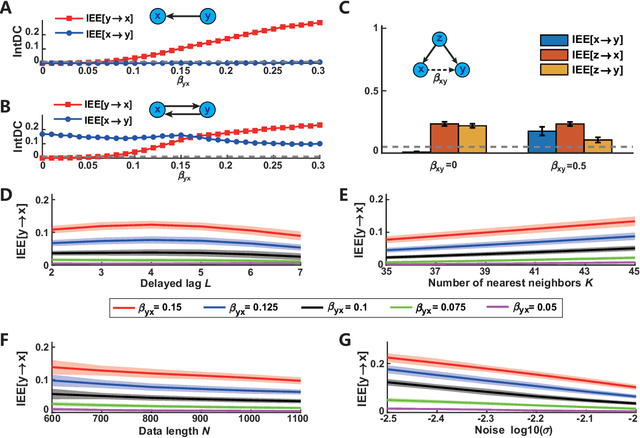
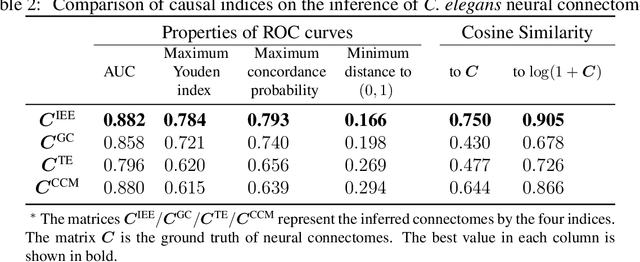
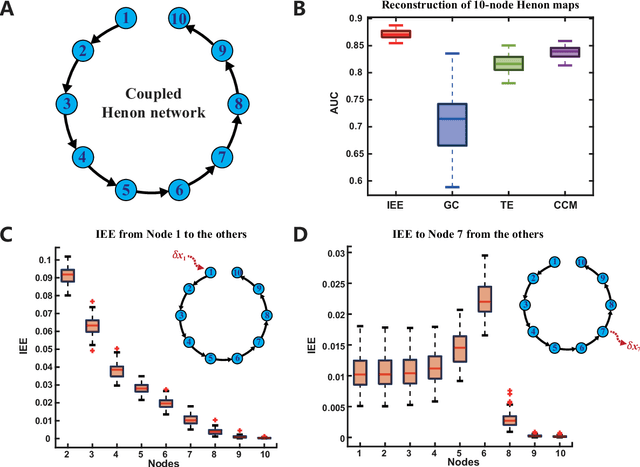
Detecting and quantifying causality is a focal topic in the fields of science, engineering, and interdisciplinary studies. However, causal studies on non-intervention systems attract much attention but remain extremely challenging. To address this challenge, we propose a framework named Interventional Dynamical Causality (IntDC) for such non-intervention systems, along with its computational criterion, Interventional Embedding Entropy (IEE), to quantify causality. The IEE criterion theoretically and numerically enables the deciphering of IntDC solely from observational (non-interventional) time-series data, without requiring any knowledge of dynamical models or real interventions in the considered system. Demonstrations of performance showed the accuracy and robustness of IEE on benchmark simulated systems as well as real-world systems, including the neural connectomes of C. elegans, COVID-19 transmission networks in Japan, and regulatory networks surrounding key circadian genes.