AKG kernel Agent: A Multi-Agent Framework for Cross-Platform Kernel Synthesis

Modern AI models demand high-performance computation kernels. The growing complexity of LLMs, multimodal architectures, and recommendation systems, combined with techniques like sparsity and quantization, creates significant computational challenges. Moreover, frequent hardware updates and diverse chip architectures further complicate this landscape, requiring tailored kernel implementations for each platform. However, manual optimization cannot keep pace with these demands, creating a critical bottleneck in AI system development. Recent advances in LLM code generation capabilities have opened new possibilities for automating kernel development. In this work, we propose AKG kernel agent (AI-driven Kernel Generator), a multi-agent system that automates kernel generation, migration, and performance tuning. AKG kernel agent is designed to support multiple domain-specific languages (DSLs), including Triton, TileLang, CPP, and CUDA-C, enabling it to target different hardware backends while maintaining correctness and portability. The system's modular design allows rapid integration of new DSLs and hardware targets. When evaluated on KernelBench using Triton DSL across GPU and NPU backends, AKG kernel agent achieves an average speedup of 1.46$\times$ over PyTorch Eager baselines implementations, demonstrating its effectiveness in accelerating kernel development for modern AI workloads.

Near-Optimal Regret for Efficient Stochastic Combinatorial Semi-Bandits

The combinatorial multi-armed bandit (CMAB) is a cornerstone of sequential decision-making framework, dominated by two algorithmic families: UCB-based and adversarial methods such as follow the regularized leader (FTRL) and online mirror descent (OMD). However, prominent UCB-based approaches like CUCB suffer from additional regret factor $\log T$ that is detrimental over long horizons, while adversarial methods such as EXP3.M and HYBRID impose significant computational overhead. To resolve this trade-off, we introduce the Combinatorial Minimax Optimal Strategy in the Stochastic setting (CMOSS). CMOSS is a computationally efficient algorithm that achieves an instance-independent regret of $O\big( (\log k)^2\sqrt{kmT}\big )$ under semi-bandit feedback, where $m$ is the number of arms and $k$ is the maximum cardinality of a feasible action. Crucially, this result eliminates the dependency on $\log T$ and matches the established $\Omega\big( \sqrt{kmT}\big)$ lower bound up to $O\big((\log k)^2\big)$. We then extend our analysis to show that CMOSS is also applicable to cascading feedback. Experiments on synthetic and real-world datasets validate that CMOSS consistently outperforms benchmark algorithms in both regret and runtime efficiency.

Tight Gap-Dependent Memory-Regret Trade-Off for Single-Pass Streaming Stochastic Multi-Armed Bandits

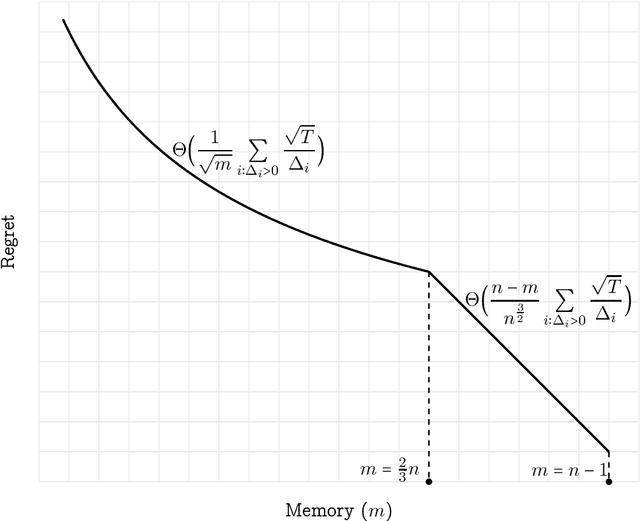
We study the problem of minimizing gap-dependent regret for single-pass streaming stochastic multi-armed bandits (MAB). In this problem, the $n$ arms are present in a stream, and at most $m<n$ arms and their statistics can be stored in the memory. We establish tight non-asymptotic regret bounds regarding all relevant parameters, including the number of arms $n$, the memory size $m$, the number of rounds $T$ and $(\Delta_i)_{i\in [n]}$ where $\Delta_i$ is the reward mean gap between the best arm and the $i$-th arm. These gaps are not known in advance by the player. Specifically, for any constant $\alpha \ge 1$, we present two algorithms: one applicable for $m\ge \frac{2}{3}n$ with regret at most $O_\alpha\Big(\frac{(n-m)T^{\frac{1}{\alpha + 1}}}{n^{1 + {\frac{1}{\alpha + 1}}}}\displaystyle\sum_{i:\Delta_i > 0}\Delta_i^{1 - 2\alpha}\Big)$ and another applicable for $m<\frac{2}{3}n$ with regret at most $O_\alpha\Big(\frac{T^{\frac{1}{\alpha+1}}}{m^{\frac{1}{\alpha+1}}}\displaystyle\sum_{i:\Delta_i > 0}\Delta_i^{1 - 2\alpha}\Big)$. We also prove matching lower bounds for both cases by showing that for any constant $\alpha\ge 1$ and any $m\leq k < n$, there exists a set of hard instances on which the regret of any algorithm is $\Omega_\alpha\Big(\frac{(k-m+1) T^{\frac{1}{\alpha+1}}}{k^{1 + \frac{1}{\alpha+1}}} \sum_{i:\Delta_i > 0}\Delta_i^{1-2\alpha}\Big)$. This is the first tight gap-dependent regret bound for streaming MAB. Prior to our work, an $O\Big(\sum_{i\colon\Delta>0} \frac{\sqrt{T}\log T}{\Delta_i}\Big)$ upper bound for the special case of $\alpha=1$ and $m=O(1)$ was established by Agarwal, Khanna and Patil (COLT'22). In contrast, our results provide the correct order of regret as $\Theta\Big(\frac{1}{\sqrt{m}}\sum_{i\colon\Delta>0}\frac{\sqrt{T}}{\Delta_i}\Big)$.

Understanding Memory-Regret Trade-Off for Streaming Stochastic Multi-Armed Bandits

We study the stochastic multi-armed bandit problem in the $P$-pass streaming model. In this problem, the $n$ arms are present in a stream and at most $m<n$ arms and their statistics can be stored in the memory. We give a complete characterization of the optimal regret in terms of $m, n$ and $P$. Specifically, we design an algorithm with $\tilde O\left((n-m)^{1+\frac{2^{P}-2}{2^{P+1}-1}} n^{\frac{2-2^{P+1}}{2^{P+1}-1}} T^{\frac{2^P}{2^{P+1}-1}}\right)$ regret and complement it with an $\tilde \Omega\left((n-m)^{1+\frac{2^{P}-2}{2^{P+1}-1}} n^{\frac{2-2^{P+1}}{2^{P+1}-1}} T^{\frac{2^P}{2^{P+1}-1}}\right)$ lower bound when the number of rounds $T$ is sufficiently large. Our results are tight up to a logarithmic factor in $n$ and $P$.