Jintong Ren
A Hierarchical Destroy and Repair Approach for Solving Very Large-Scale Travelling Salesman Problem
Aug 09, 2023
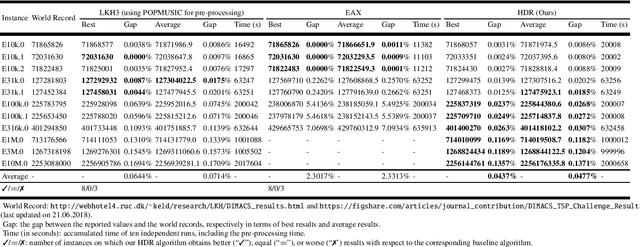
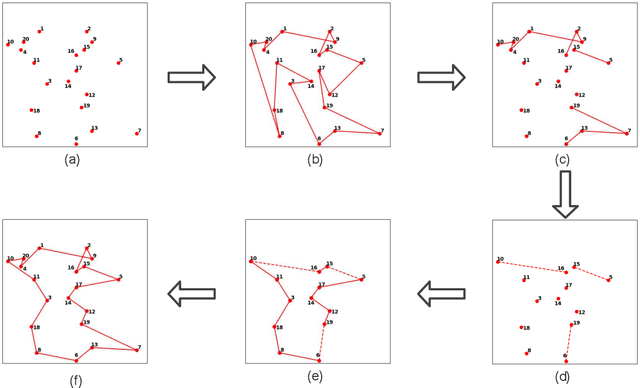
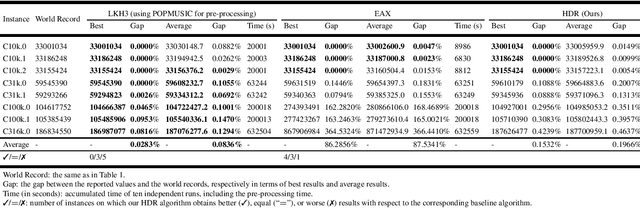
Abstract:For prohibitively large-scale Travelling Salesman Problems (TSPs), existing algorithms face big challenges in terms of both computational efficiency and solution quality. To address this issue, we propose a hierarchical destroy-and-repair (HDR) approach, which attempts to improve an initial solution by applying a series of carefully designed destroy-and-repair operations. A key innovative concept is the hierarchical search framework, which recursively fixes partial edges and compresses the input instance into a small-scale TSP under some equivalence guarantee. This neat search framework is able to deliver highly competitive solutions within a reasonable time. Fair comparisons based on nineteen famous large-scale instances (with 10,000 to 10,000,000 cities) show that HDR is highly competitive against existing state-of-the-art TSP algorithms, in terms of both efficiency and solution quality. Notably, on two large instances with 3,162,278 and 10,000,000 cities, HDR breaks the world records (i.e., best-known results regardless of computation time), which were previously achieved by LKH and its variants, while HDR is completely independent of LKH. Finally, ablation studies are performed to certify the importance and validity of the hierarchical search framework.
An effective hybrid search algorithm for the multiple traveling repairman problem with profits
Nov 09, 2021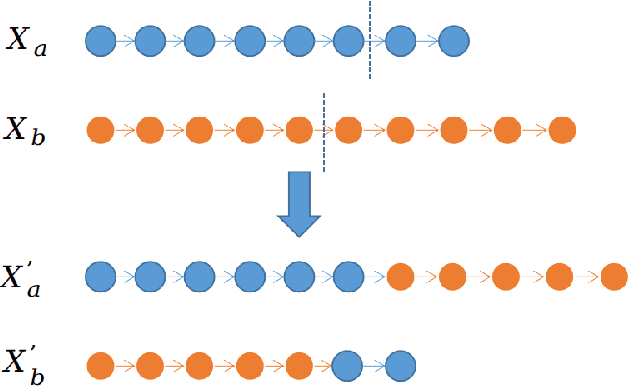


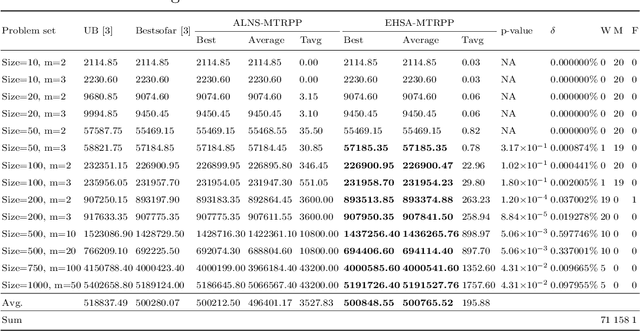
Abstract:As an extension of the traveling repairman problem with profits, the multiple traveling repairman problem with profits consists of multiple repairmen who visit a subset of all customers to maximize the revenues collected through the visited customers. To solve this challenging problem, an effective hybrid search algorithm based on the memetic algorithm framework is proposed. It integrates two distinguished features: a dedicated arc-based crossover to generate high-quality offspring solutions and a fast evaluation technique to reduce the complexity of exploring the classical neighborhoods. We show the competitiveness of the algorithm on 470 benchmark instances compared to the leading reference algorithms and report new best records for 137 instances as well as equal best results for other 330 instances. We investigate the importance of the key search components for the algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge