A Hierarchical Destroy and Repair Approach for Solving Very Large-Scale Travelling Salesman Problem

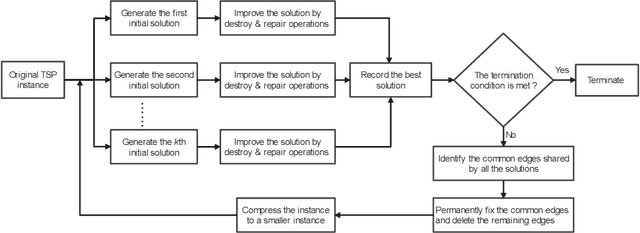
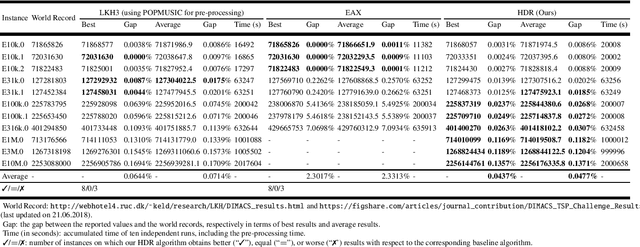
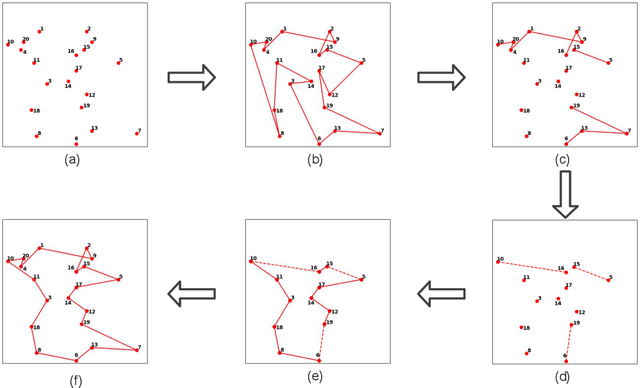
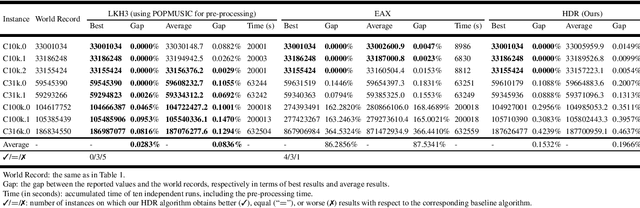
For prohibitively large-scale Travelling Salesman Problems (TSPs), existing algorithms face big challenges in terms of both computational efficiency and solution quality. To address this issue, we propose a hierarchical destroy-and-repair (HDR) approach, which attempts to improve an initial solution by applying a series of carefully designed destroy-and-repair operations. A key innovative concept is the hierarchical search framework, which recursively fixes partial edges and compresses the input instance into a small-scale TSP under some equivalence guarantee. This neat search framework is able to deliver highly competitive solutions within a reasonable time. Fair comparisons based on nineteen famous large-scale instances (with 10,000 to 10,000,000 cities) show that HDR is highly competitive against existing state-of-the-art TSP algorithms, in terms of both efficiency and solution quality. Notably, on two large instances with 3,162,278 and 10,000,000 cities, HDR breaks the world records (i.e., best-known results regardless of computation time), which were previously achieved by LKH and its variants, while HDR is completely independent of LKH. Finally, ablation studies are performed to certify the importance and validity of the hierarchical search framework.

Feature Importance-aware Graph Attention Network and Dueling Double Deep Q-Network Combined Approach for Critical Node Detection Problems

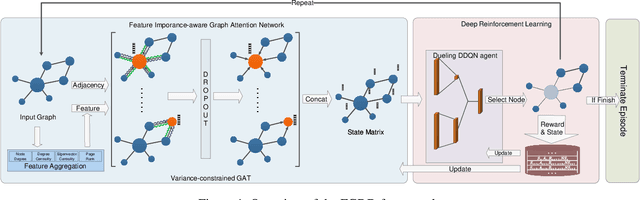
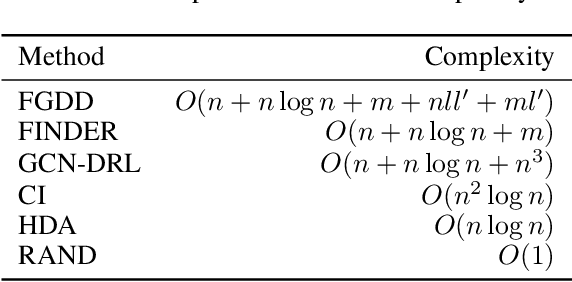
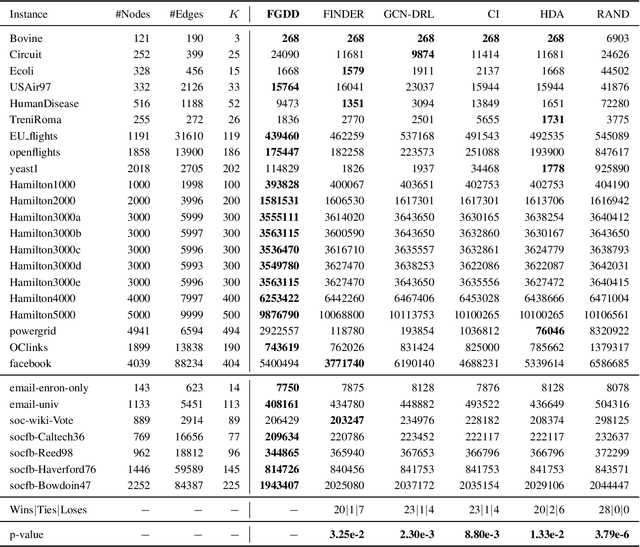
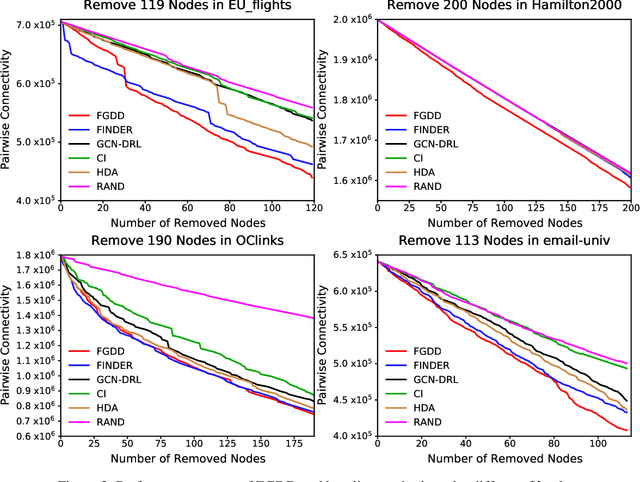
Detecting critical nodes in sparse networks is important in a variety of application domains. A Critical Node Problem (CNP) aims to find a set of critical nodes from a network whose deletion maximally degrades the pairwise connectivity of the residual network. Due to its general NP-hard nature, state-of-the-art CNP solutions are based on heuristic approaches. Domain knowledge and trial-and-error are usually required when designing such approaches, thus consuming considerable effort and time. This work proposes a feature importance-aware graph attention network for node representation and combines it with dueling double deep Q-network to create an end-to-end algorithm to solve CNP for the first time. It does not need any problem-specific knowledge or labeled datasets as required by most of existing methods. Once the model is trained, it can be generalized to cope with various types of CNPs (with different sizes and topological structures) without re-training. Extensive experiments on 28 real-world networks show that the proposed method is highly comparable to state-of-the-art methods. It does not require any problem-specific knowledge and, hence, can be applicable to many applications including those impossible ones by using the existing approaches. It can be combined with some local search methods to further improve its solution quality. Extensive comparison results are given to show its effectiveness in solving CNP.

An effective hybrid search algorithm for the multiple traveling repairman problem with profits

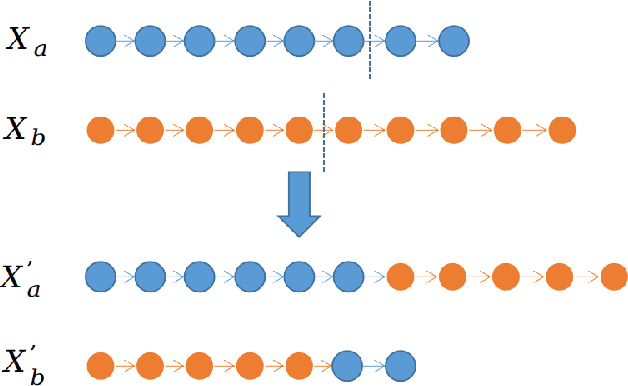
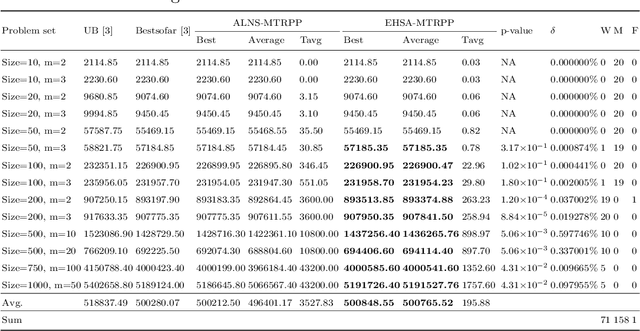
As an extension of the traveling repairman problem with profits, the multiple traveling repairman problem with profits consists of multiple repairmen who visit a subset of all customers to maximize the revenues collected through the visited customers. To solve this challenging problem, an effective hybrid search algorithm based on the memetic algorithm framework is proposed. It integrates two distinguished features: a dedicated arc-based crossover to generate high-quality offspring solutions and a fast evaluation technique to reduce the complexity of exploring the classical neighborhoods. We show the competitiveness of the algorithm on 470 benchmark instances compared to the leading reference algorithms and report new best records for 137 instances as well as equal best results for other 330 instances. We investigate the importance of the key search components for the algorithm.

Generalize a Small Pre-trained Model to Arbitrarily Large TSP Instances

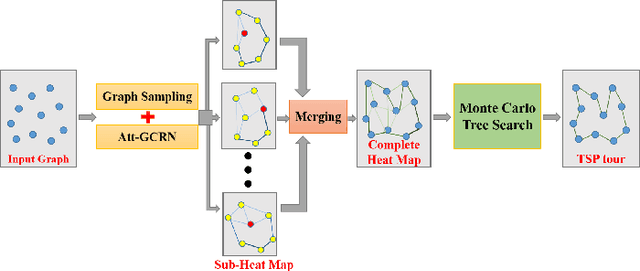
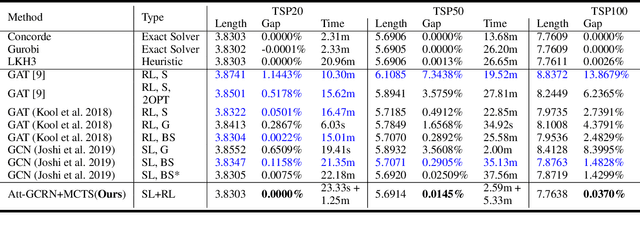
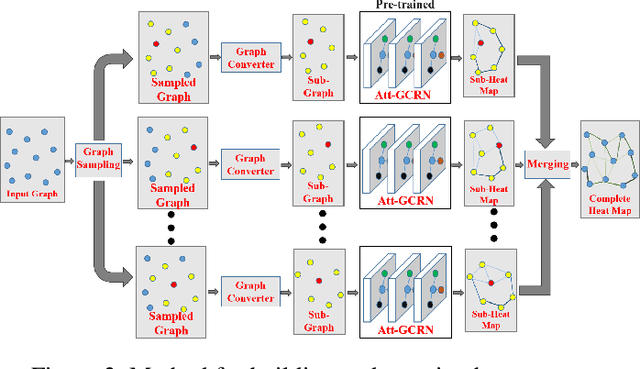
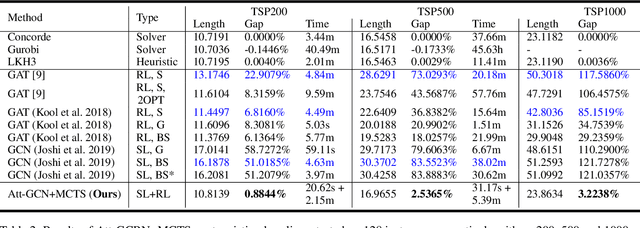
For the traveling salesman problem (TSP), the existing supervised learning based algorithms suffer seriously from the lack of generalization ability. To overcome this drawback, this paper tries to train (in supervised manner) a small-scale model, which could be repetitively used to build heat maps for TSP instances of arbitrarily large size, based on a series of techniques such as graph sampling, graph converting and heat maps merging. Furthermore, the heat maps are fed into a reinforcement learning approach (Monte Carlo tree search), to guide the search of high-quality solutions. Experimental results based on a large number of instances (with up to 10,000 vertices) show that, this new approach clearly outperforms the existing machine learning based TSP algorithms, and significantly improves the generalization ability of the trained model.

Variable Population Memetic Search: A Case Study on the Critical Node Problem

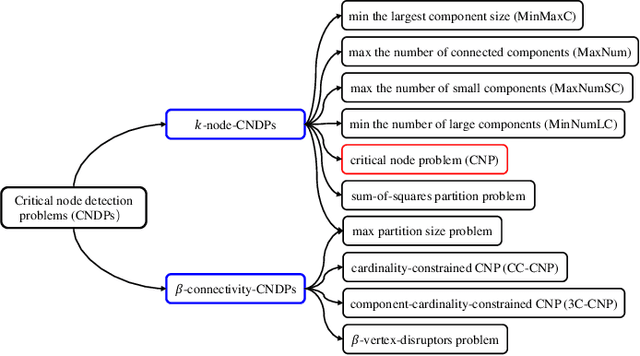
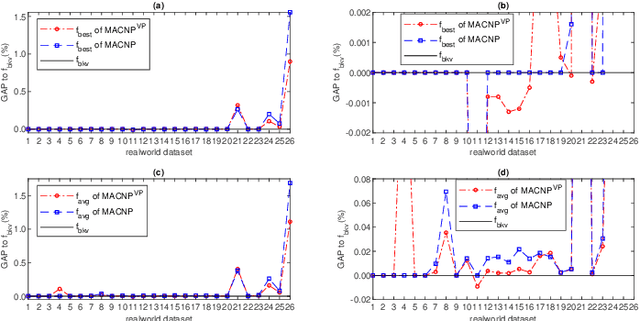
Population-based memetic algorithms have been successfully applied to solve many difficult combinatorial problems. Often, a population of fixed size was used in such algorithms to record some best solutions sampled during the search. However, given the particular features of the problem instance under consideration, a population of variable size would be more suitable to ensure the best search performance possible. In this work, we propose variable population memetic search (VPMS), where a strategic population sizing mechanism is used to dynamically adjust the population size during the memetic search process. Our VPMS approach starts its search from a small population of only two solutions to focus on exploitation, and then adapts the population size according to the search status to continuously influence the balancing between exploitation and exploration. We illustrate an application of the VPMS approach to solve the challenging critical node problem (CNP). We show that the VPMS algorithm integrating a variable population, an effective local optimization procedure (called diversified late acceptance search) and a backbone-based crossover operator performs very well compared to state-of-the-art CNP algorithms. The algorithm is able to discover new upper bounds for 13 instances out of the 42 popular benchmark instances, while matching 23 previous best-known upper bounds.

A Three-Phase Search Approach for the Quadratic Minimum Spanning Tree Problem

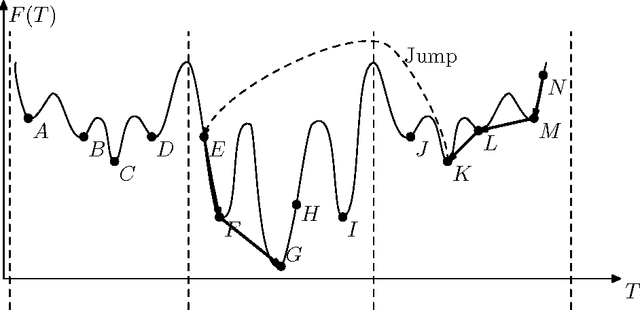
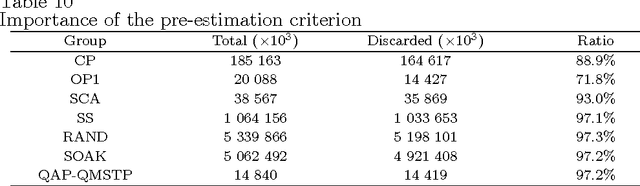
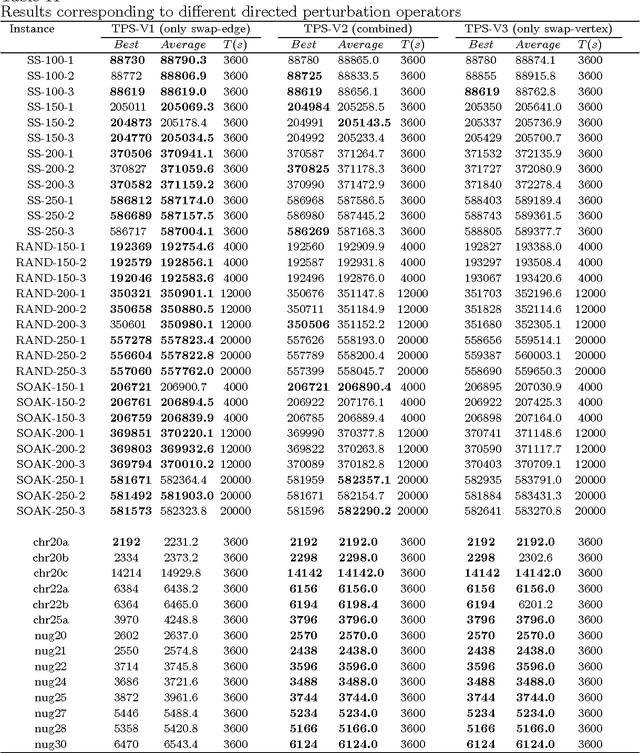
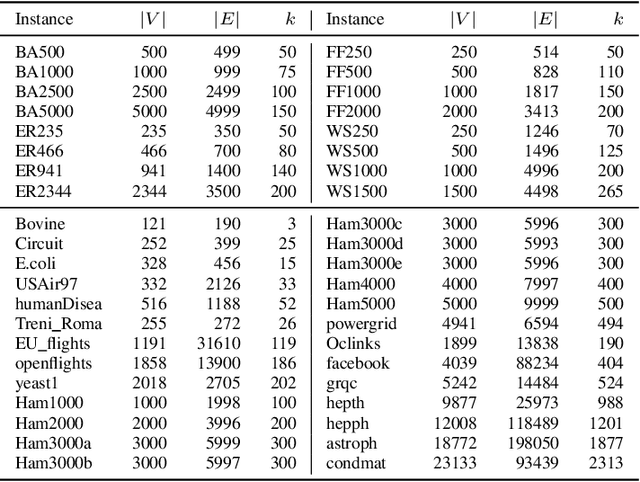
Given an undirected graph with costs associated with each edge as well as each pair of edges, the quadratic minimum spanning tree problem (QMSTP) consists of determining a spanning tree of minimum total cost. This problem can be used to model many real-life network design applications, in which both routing and interference costs should be considered. For this problem, we propose a three-phase search approach named TPS, which integrates 1) a descent-based neighborhood search phase using two different move operators to reach a local optimum from a given starting solution, 2) a local optima exploring phase to discover nearby local optima within a given regional search area, and 3) a perturbation-based diversification phase to jump out of the current regional search area. Additionally, we introduce dedicated techniques to reduce the neighborhood to explore and streamline the neighborhood evaluations. Computational experiments based on hundreds of representative benchmarks show that TPS produces highly competitive results with respect to the best performing approaches in the literature by improving the best known results for 31 instances and matching the best known results for the remaining instances only except two cases. Critical elements of the proposed algorithms are analyzed.