Variable Population Memetic Search: A Case Study on the Critical Node Problem

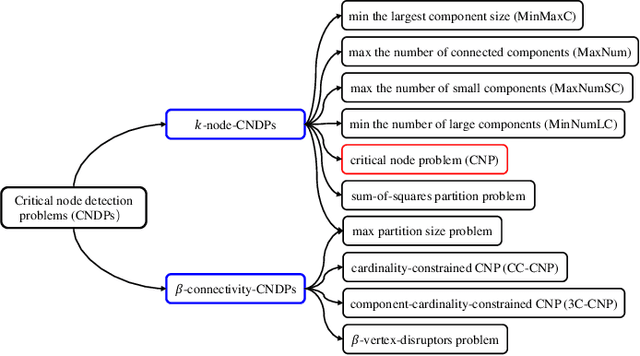
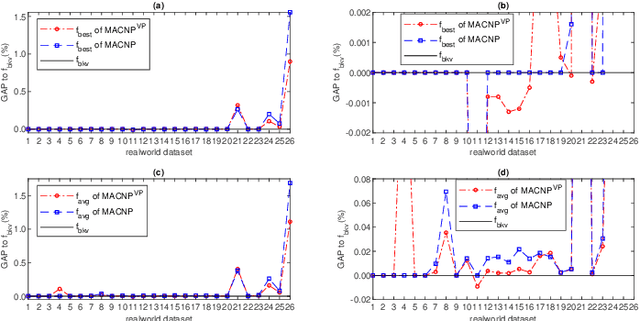
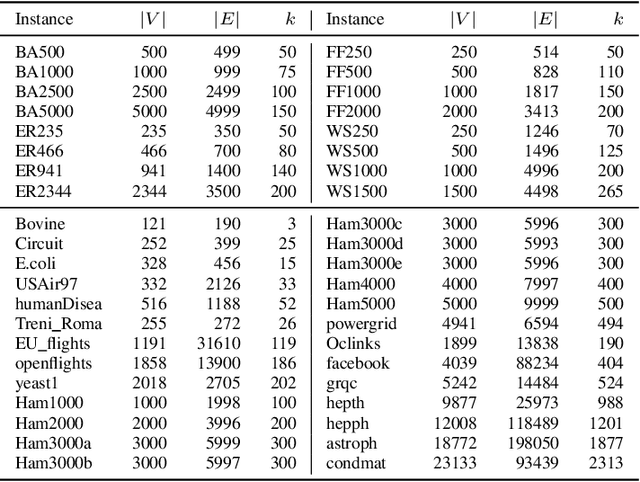
Population-based memetic algorithms have been successfully applied to solve many difficult combinatorial problems. Often, a population of fixed size was used in such algorithms to record some best solutions sampled during the search. However, given the particular features of the problem instance under consideration, a population of variable size would be more suitable to ensure the best search performance possible. In this work, we propose variable population memetic search (VPMS), where a strategic population sizing mechanism is used to dynamically adjust the population size during the memetic search process. Our VPMS approach starts its search from a small population of only two solutions to focus on exploitation, and then adapts the population size according to the search status to continuously influence the balancing between exploitation and exploration. We illustrate an application of the VPMS approach to solve the challenging critical node problem (CNP). We show that the VPMS algorithm integrating a variable population, an effective local optimization procedure (called diversified late acceptance search) and a backbone-based crossover operator performs very well compared to state-of-the-art CNP algorithms. The algorithm is able to discover new upper bounds for 13 instances out of the 42 popular benchmark instances, while matching 23 previous best-known upper bounds.

On memetic search for the max-mean dispersion problem

Given a set $V$ of $n$ elements and a distance matrix $[d_{ij}]_{n\times n}$ among elements, the max-mean dispersion problem (MaxMeanDP) consists in selecting a subset $M$ from $V$ such that the mean dispersion (or distance) among the selected elements is maximized. Being a useful model to formulate several relevant applications, MaxMeanDP is known to be NP-hard and thus computationally difficult. In this paper, we present a highly effective memetic algorithm for MaxMeanDP which relies on solution recombination and local optimization to find high quality solutions. Computational experiments on the set of 160 benchmark instances with up to 1000 elements commonly used in the literature show that the proposed algorithm improves or matches the published best known results for all instances in a short computing time, with only one exception, while achieving a high success rate of 100\%. In particular, we improve 59 previous best results out of the 60 most challenging instances. Results on a set of 40 new large instances with 3000 and 5000 elements are also presented. The key ingredients of the proposed algorithm are investigated to shed light on how they affect the performance of the algorithm.