Near-Optimal Quantum Coreset Construction Algorithms for Clustering

$k$-Clustering in $\mathbb{R}^d$ (e.g., $k$-median and $k$-means) is a fundamental machine learning problem. While near-linear time approximation algorithms were known in the classical setting for a dataset with cardinality $n$, it remains open to find sublinear-time quantum algorithms. We give quantum algorithms that find coresets for $k$-clustering in $\mathbb{R}^d$ with $\tilde{O}(\sqrt{nk}d^{3/2})$ query complexity. Our coreset reduces the input size from $n$ to $\mathrm{poly}(k\epsilon^{-1}d)$, so that existing $\alpha$-approximation algorithms for clustering can run on top of it and yield $(1 + \epsilon)\alpha$-approximation. This eventually yields a quadratic speedup for various $k$-clustering approximation algorithms. We complement our algorithm with a nearly matching lower bound, that any quantum algorithm must make $\Omega(\sqrt{nk})$ queries in order to achieve even $O(1)$-approximation for $k$-clustering.

On The Relative Error of Random Fourier Features for Preserving Kernel Distance

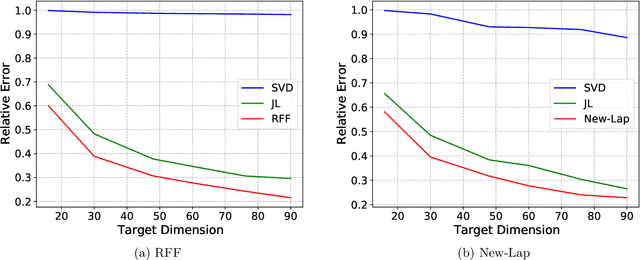
The method of random Fourier features (RFF), proposed in a seminal paper by Rahimi and Recht (NIPS'07), is a powerful technique to find approximate low-dimensional representations of points in (high-dimensional) kernel space, for shift-invariant kernels. While RFF has been analyzed under various notions of error guarantee, the ability to preserve the kernel distance with \emph{relative} error is less understood. We show that for a significant range of kernels, including the well-known Laplacian kernels, RFF cannot approximate the kernel distance with small relative error using low dimensions. We complement this by showing as long as the shift-invariant kernel is analytic, RFF with $\mathrm{poly}(\epsilon^{-1} \log n)$ dimensions achieves $\epsilon$-relative error for pairwise kernel distance of $n$ points, and the dimension bound is improved to $\mathrm{poly}(\epsilon^{-1}\log k)$ for the specific application of kernel $k$-means. Finally, going beyond RFF, we make the first step towards data-oblivious dimension-reduction for general shift-invariant kernels, and we obtain a similar $\mathrm{poly}(\epsilon^{-1} \log n)$ dimension bound for Laplacian kernels. We also validate the dimension-error tradeoff of our methods on simulated datasets, and they demonstrate superior performance compared with other popular methods including random-projection and Nystr\"{o}m methods.

Coresets for Clustering with Fairness Constraints

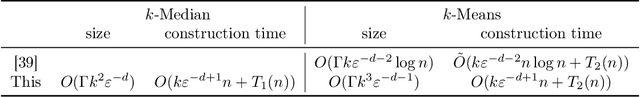
In a recent work, [19] studied the following "fair" variants of classical clustering problems such as $k$-means and $k$-median: given a set of $n$ data points in $\mathbb{R}^d$ and a binary type associated to each data point, the goal is to cluster the points while ensuring that the proportion of each type in each cluster is roughly the same as its underlying proportion. Subsequent work has focused on either extending this setting to when each data point has multiple, non-disjoint sensitive types such as race and gender [6], or to address the problem that the clustering algorithms in the above work do not scale well. The main contribution of this paper is an approach to clustering with fairness constraints that involve multiple, non-disjoint types, that is also scalable. Our approach is based on novel constructions of coresets: for the $k$-median objective, we construct an $\varepsilon$-coreset of size $O(\Gamma k^2 \varepsilon^{-d})$ where $\Gamma$ is the number of distinct collections of groups that a point may belong to, and for the $k$-means objective, we show how to construct an $\varepsilon$-coreset of size $O(\Gamma k^3\varepsilon^{-d-1})$. The former result is the first known coreset construction for the fair clustering problem with the $k$-median objective, and the latter result removes the dependence on the size of the full dataset as in [39] and generalizes it to multiple, non-disjoint types. Plugging our coresets into existing algorithms for fair clustering such as [5] results in the fastest algorithms for several cases. Empirically, we assess our approach over the \textbf{Adult}, \textbf{Bank} and \textbf{Diabetes} dataset, and show that the coreset sizes are much smaller than the full dataset. We also achieve a speed-up to recent fair clustering algorithms [5,6] on a large dataset \textbf{Census1990} by incorporating our coreset construction.