On The Relative Error of Random Fourier Features for Preserving Kernel Distance

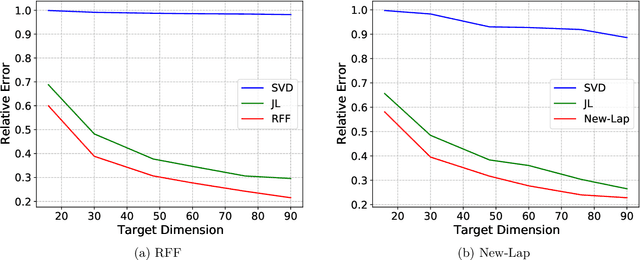
The method of random Fourier features (RFF), proposed in a seminal paper by Rahimi and Recht (NIPS'07), is a powerful technique to find approximate low-dimensional representations of points in (high-dimensional) kernel space, for shift-invariant kernels. While RFF has been analyzed under various notions of error guarantee, the ability to preserve the kernel distance with \emph{relative} error is less understood. We show that for a significant range of kernels, including the well-known Laplacian kernels, RFF cannot approximate the kernel distance with small relative error using low dimensions. We complement this by showing as long as the shift-invariant kernel is analytic, RFF with $\mathrm{poly}(\epsilon^{-1} \log n)$ dimensions achieves $\epsilon$-relative error for pairwise kernel distance of $n$ points, and the dimension bound is improved to $\mathrm{poly}(\epsilon^{-1}\log k)$ for the specific application of kernel $k$-means. Finally, going beyond RFF, we make the first step towards data-oblivious dimension-reduction for general shift-invariant kernels, and we obtain a similar $\mathrm{poly}(\epsilon^{-1} \log n)$ dimension bound for Laplacian kernels. We also validate the dimension-error tradeoff of our methods on simulated datasets, and they demonstrate superior performance compared with other popular methods including random-projection and Nystr\"{o}m methods.

Bounded Incentives in Manipulating the Probabilistic Serial Rule

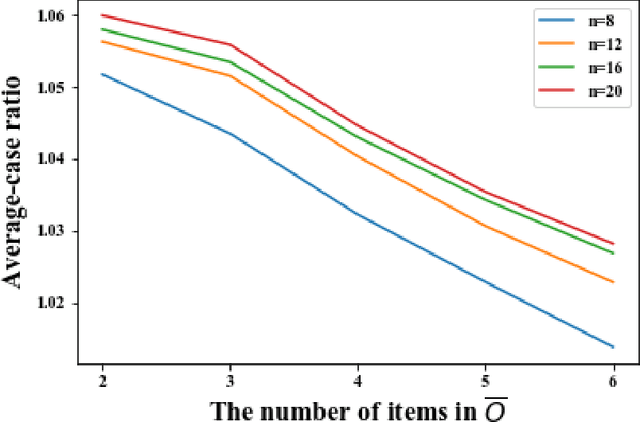
The Probabilistic Serial mechanism is well-known for its desirable fairness and efficiency properties. It is one of the most prominent protocols for the random assignment problem. However, Probabilistic Serial is not incentive-compatible, thereby these desirable properties only hold for the agents' declared preferences, rather than their genuine preferences. A substantial utility gain through strategic behaviors would trigger self-interested agents to manipulate the mechanism and would subvert the very foundation of adopting the mechanism in practice. In this paper, we characterize the extent to which an individual agent can increase its utility by strategic manipulation. We show that the incentive ratio of the mechanism is $\frac{3}{2}$. That is, no agent can misreport its preferences such that its utility becomes more than 1.5 times of what it is when reports truthfully. This ratio is a worst-case guarantee by allowing an agent to have complete information about other agents' reports and to figure out the best response strategy even if it is computationally intractable in general. To complement this worst-case study, we further evaluate an agent's utility gain on average by experiments. The experiments show that an agent' incentive in manipulating the rule is very limited. These results shed some light on the robustness of Probabilistic Serial against strategic manipulation, which is one step further than knowing that it is not incentive-compatible.