Coresets for Clustering with Fairness Constraints

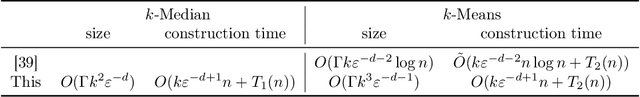
In a recent work, [19] studied the following "fair" variants of classical clustering problems such as $k$-means and $k$-median: given a set of $n$ data points in $\mathbb{R}^d$ and a binary type associated to each data point, the goal is to cluster the points while ensuring that the proportion of each type in each cluster is roughly the same as its underlying proportion. Subsequent work has focused on either extending this setting to when each data point has multiple, non-disjoint sensitive types such as race and gender [6], or to address the problem that the clustering algorithms in the above work do not scale well. The main contribution of this paper is an approach to clustering with fairness constraints that involve multiple, non-disjoint types, that is also scalable. Our approach is based on novel constructions of coresets: for the $k$-median objective, we construct an $\varepsilon$-coreset of size $O(\Gamma k^2 \varepsilon^{-d})$ where $\Gamma$ is the number of distinct collections of groups that a point may belong to, and for the $k$-means objective, we show how to construct an $\varepsilon$-coreset of size $O(\Gamma k^3\varepsilon^{-d-1})$. The former result is the first known coreset construction for the fair clustering problem with the $k$-median objective, and the latter result removes the dependence on the size of the full dataset as in [39] and generalizes it to multiple, non-disjoint types. Plugging our coresets into existing algorithms for fair clustering such as [5] results in the fastest algorithms for several cases. Empirically, we assess our approach over the \textbf{Adult}, \textbf{Bank} and \textbf{Diabetes} dataset, and show that the coreset sizes are much smaller than the full dataset. We also achieve a speed-up to recent fair clustering algorithms [5,6] on a large dataset \textbf{Census1990} by incorporating our coreset construction.