Optimizing Through Change: Bounds and Recommendations for Time-Varying Bayesian Optimization Algorithms

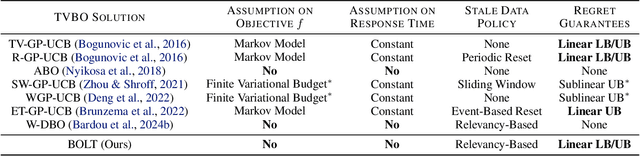
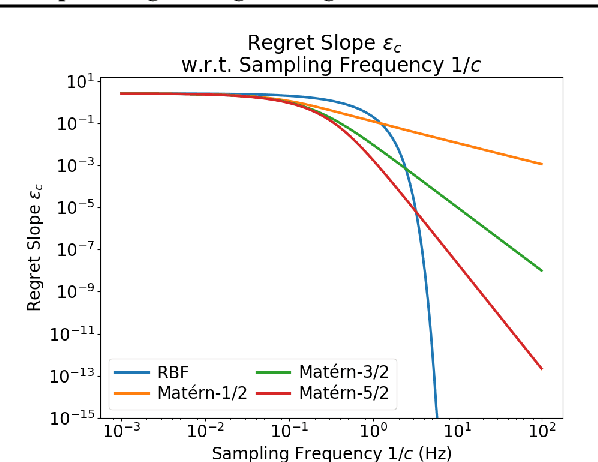
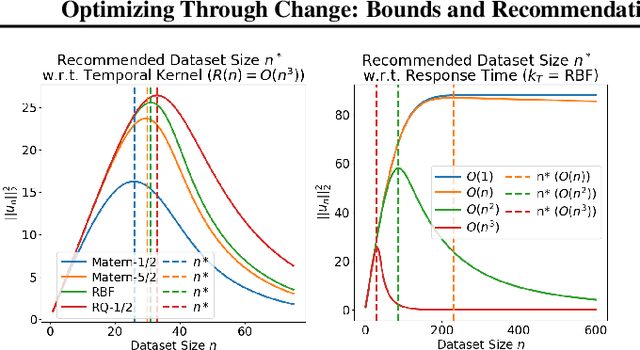
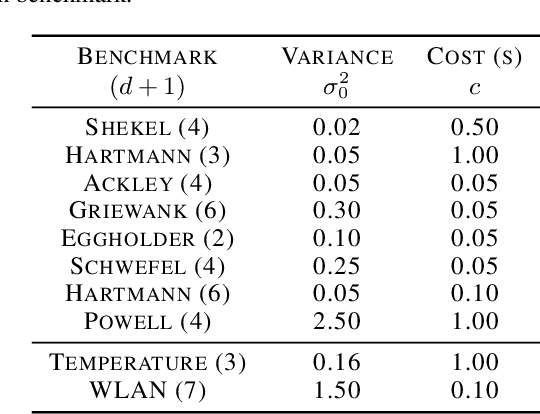
Time-Varying Bayesian Optimization (TVBO) is the go-to framework for optimizing a time-varying, expensive, noisy black-box function. However, most of the solutions proposed so far either rely on unrealistic assumptions on the nature of the objective function or do not offer any theoretical guarantees. We propose the first analysis that asymptotically bounds the cumulative regret of TVBO algorithms under mild and realistic assumptions only. In particular, we provide an algorithm-independent lower regret bound and an upper regret bound that holds for a large class of TVBO algorithms. Based on this analysis, we formulate recommendations for TVBO algorithms and show how an algorithm (BOLT) that follows them performs better than the state-of-the-art of TVBO through experiments on synthetic and real-world problems.

This Too Shall Pass: Removing Stale Observations in Dynamic Bayesian Optimization

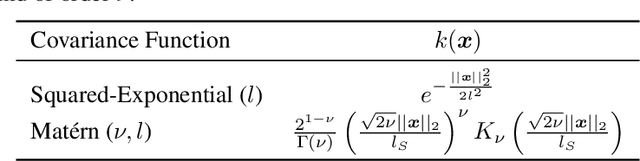
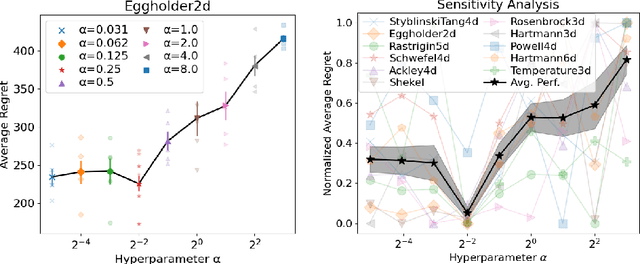
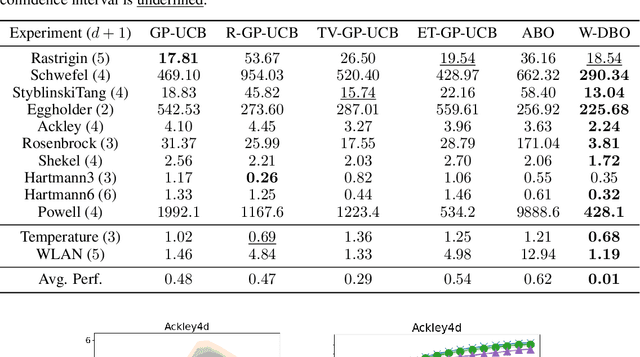
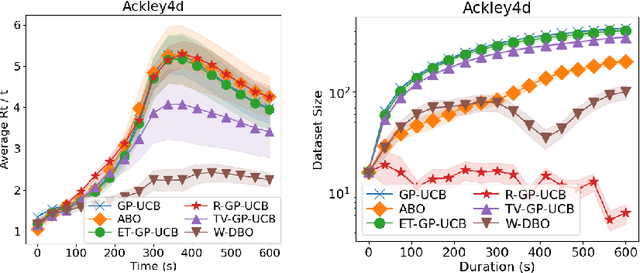
Bayesian Optimization (BO) has proven to be very successful at optimizing a static, noisy, costly-to-evaluate black-box function $f : \mathcal{S} \to \mathbb{R}$. However, optimizing a black-box which is also a function of time (i.e., a dynamic function) $f : \mathcal{S} \times \mathcal{T} \to \mathbb{R}$ remains a challenge, since a dynamic Bayesian Optimization (DBO) algorithm has to keep track of the optimum over time. This changes the nature of the optimization problem in at least three aspects: (i) querying an arbitrary point in $\mathcal{S} \times \mathcal{T}$ is impossible, (ii) past observations become less and less relevant for keeping track of the optimum as time goes by and (iii) the DBO algorithm must have a high sampling frequency so it can collect enough relevant observations to keep track of the optimum through time. In this paper, we design a Wasserstein distance-based criterion able to quantify the relevancy of an observation with respect to future predictions. Then, we leverage this criterion to build W-DBO, a DBO algorithm able to remove irrelevant observations from its dataset on the fly, thus maintaining simultaneously a good predictive performance and a high sampling frequency, even in continuous-time optimization tasks with unknown horizon. Numerical experiments establish the superiority of W-DBO, which outperforms state-of-the-art methods by a comfortable margin.

Relaxing the Additivity Constraints in Decentralized No-Regret High-Dimensional Bayesian Optimization

Bayesian Optimization (BO) is typically used to optimize an unknown function $f$ that is noisy and costly to evaluate, by exploiting an acquisition function that must be maximized at each optimization step. Although provably asymptotically optimal BO algorithms are efficient at optimizing low-dimensional functions, scaling them to high-dimensional spaces remains an open research problem, often tackled by assuming an additive structure for $f$. However, such algorithms introduce additional restrictive assumptions on the additive structure that reduce their applicability domain. In this paper, we relax the restrictive assumptions on the additive structure of $f$, at the expense of weakening the maximization guarantees of the acquisition function, and we address the over-exploration problem for decentralized BO algorithms. To these ends, we propose DuMBO, an asymptotically optimal decentralized BO algorithm that achieves very competitive performance against state-of-the-art BO algorithms, especially when the additive structure of $f$ does not exist or comprises high-dimensional factors.