Many Experiments, Few Repetitions, Unpaired Data, and Sparse Effects: Is Causal Inference Possible?

We study the problem of estimating causal effects under hidden confounding in the following unpaired data setting: we observe some covariates $X$ and an outcome $Y$ under different experimental conditions (environments) but do not observe them jointly; we either observe $X$ or $Y$. Under appropriate regularity conditions, the problem can be cast as an instrumental variable (IV) regression with the environment acting as a (possibly high-dimensional) instrument. When there are many environments but only a few observations per environment, standard two-sample IV estimators fail to be consistent. We propose a GMM-type estimator based on cross-fold sample splitting of the instrument-covariate sample and prove that it is consistent as the number of environments grows but the sample size per environment remains constant. We further extend the method to sparse causal effects via $\ell_1$-regularized estimation and post-selection refitting.

Transferring Causal Effects using Proxies

We consider the problem of estimating a causal effect in a multi-domain setting. The causal effect of interest is confounded by an unobserved confounder and can change between the different domains. We assume that we have access to a proxy of the hidden confounder and that all variables are discrete or categorical. We propose methodology to estimate the causal effect in the target domain, where we assume to observe only the proxy variable. Under these conditions, we prove identifiability (even when treatment and response variables are continuous). We introduce two estimation techniques, prove consistency, and derive confidence intervals. The theoretical results are supported by simulation studies and a real-world example studying the causal effect of website rankings on consumer choices.

DecoR: Deconfounding Time Series with Robust Regression

Causal inference on time series data is a challenging problem, especially in the presence of unobserved confounders. This work focuses on estimating the causal effect between two time series, which are confounded by a third, unobserved time series. Assuming spectral sparsity of the confounder, we show how in the frequency domain this problem can be framed as an adversarial outlier problem. We introduce Deconfounding by Robust regression (DecoR), a novel approach that estimates the causal effect using robust linear regression in the frequency domain. Considering two different robust regression techniques, we first improve existing bounds on the estimation error for such techniques. Crucially, our results do not require distributional assumptions on the covariates. We can therefore use them in time series settings. Applying these results to DecoR, we prove, under suitable assumptions, upper bounds for the estimation error of DecoR that imply consistency. We show DecoR's effectiveness through experiments on synthetic data. Our experiments furthermore suggest that our method is robust with respect to model misspecification.

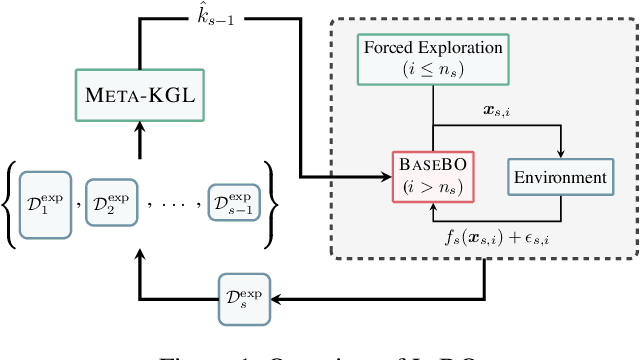
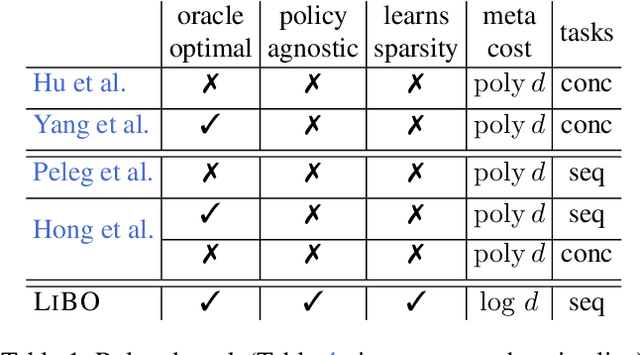
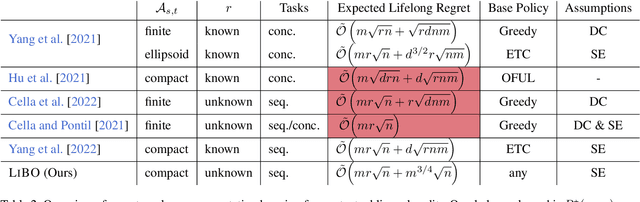
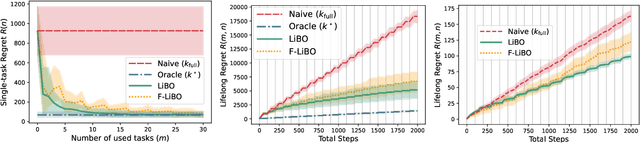
Lifelong Bandit Optimization: No Prior and No Regret

In practical applications, machine learning algorithms are often repeatedly applied to problems with similar structure over and over again. We focus on solving a sequence of bandit optimization tasks and develop LiBO, an algorithm which adapts to the environment by learning from past experience and becoming more sample-efficient in the process. We assume a kernelized structure where the kernel is unknown but shared across all tasks. LiBO sequentially meta-learns a kernel that approximates the true kernel and simultaneously solves the incoming tasks with the latest kernel estimate. Our algorithm can be paired with any kernelized bandit algorithm and guarantees oracle optimal performance, meaning that as more tasks are solved, the regret of LiBO on each task converges to the regret of the bandit algorithm with oracle knowledge of the true kernel. Naturally, if paired with a sublinear bandit algorithm, LiBO yields a sublinear lifelong regret. We also show that direct access to the data from each task is not necessary for attaining sublinear regret. The lifelong problem can thus be solved in a federated manner, while keeping the data of each task private.