Revisiting Sanity Checks for Saliency Maps

Saliency methods are a popular approach for model debugging and explainability. However, in the absence of ground-truth data for what the correct maps should be, evaluating and comparing different approaches remains a long-standing challenge. The sanity checks methodology of Adebayo et al [Neurips 2018] has sought to address this challenge. They argue that some popular saliency methods should not be used for explainability purposes since the maps they produce are not sensitive to the underlying model that is to be explained. Through a causal re-framing of their objective, we argue that their empirical evaluation does not fully establish these conclusions, due to a form of confounding introduced by the tasks they evaluate on. Through various experiments on simple custom tasks we demonstrate that some of their conclusions may indeed be artifacts of the tasks more than a criticism of the saliency methods themselves. More broadly, our work challenges the utility of the sanity check methodology, and further highlights that saliency map evaluation beyond ad-hoc visual examination remains a fundamental challenge.

On Calibration and Out-of-domain Generalization

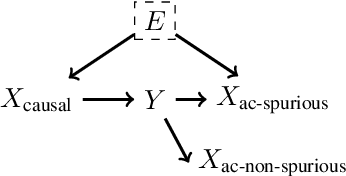
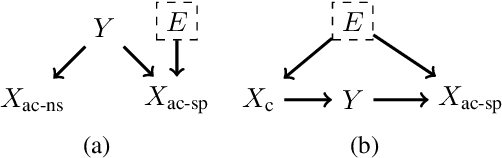
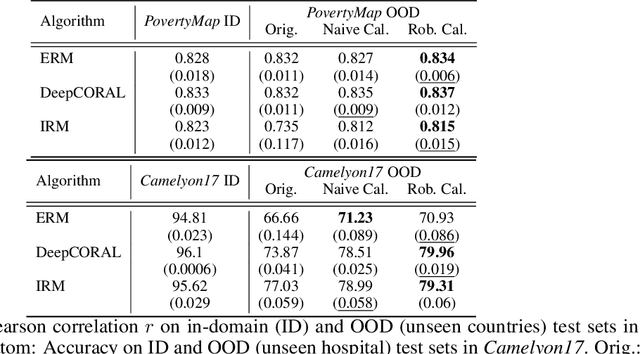
Out-of-domain (OOD) generalization is a significant challenge for machine learning models. To overcome it, many novel techniques have been proposed, often focused on learning models with certain invariance properties. In this work, we draw a link between OOD performance and model calibration, arguing that calibration across multiple domains can be viewed as a special case of an invariant representation leading to better OOD generalization. Specifically, we prove in a simplified setting that models which achieve multi-domain calibration are free of spurious correlations. This leads us to propose multi-domain calibration as a measurable surrogate for the OOD performance of a classifier. An important practical benefit of calibration is that there are many effective tools for calibrating classifiers. We show that these tools are easy to apply and adapt for a multi-domain setting. Using five datasets from the recently proposed WILDS OOD benchmark we demonstrate that simply re-calibrating models across multiple domains in a validation set leads to significantly improved performance on unseen test domains. We believe this intriguing connection between calibration and OOD generalization is promising from a practical point of view and deserves further research from a theoretical point of view.

Robust learning with the Hilbert-Schmidt independence criterion

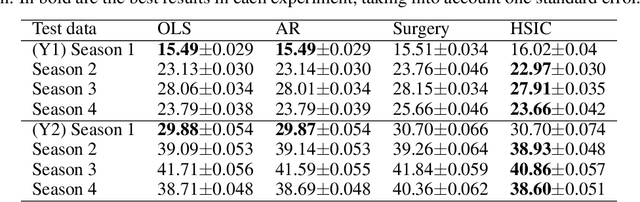
We investigate the use of a non-parametric independence measure, the Hilbert-Schmidt Independence Criterion (HSIC), as a loss-function for learning robust regression and classification models. This loss-function encourages learning models where the distribution of the residuals between the label and the model-prediction is statistically independent of the distribution of the instances themselves. This loss-function was first proposed by Mooij et al. [2009] in the context of learning causal graphs. We adapt it to the task of robust learning for unsupervised covariate shift: learning on a source domain without access to any instances or labels from the unknown target domain. We prove that the proposed loss is expected to generalize to a class of target domains described in terms of the complexity of their density ratio function with respect to the source domain. Experiments on tasks of unsupervised covariate shift demonstrate that models learned with the proposed loss-function outperform several baseline methods.

Learning to Optimize Multigrid PDE Solvers

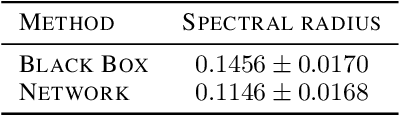
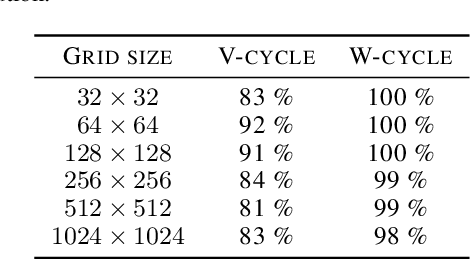
Constructing fast numerical solvers for partial differential equations (PDEs) is crucial for many scientific disciplines. A leading technique for solving large-scale PDEs is using multigrid methods. At the core of a multigrid solver is the prolongation matrix, which relates between different scales of the problem. This matrix is strongly problem-dependent, and its optimal construction is critical to the efficiency of the solver. In practice, however, devising multigrid algorithms for new problems often poses formidable challenges. In this paper we propose a framework for learning multigrid solvers. Our method learns a (single) mapping from discretized PDEs to prolongation operators for a broad class of 2D diffusion problems. We train a neural network once for the entire class of PDEs, using an efficient and unsupervised loss function. Our tests demonstrate improved convergence rates compared to the widely used Black-Box multigrid scheme, suggesting that our method successfully learned rules for constructing prolongation matrices.

Improved Training for Self-Training by Confidence Assessments

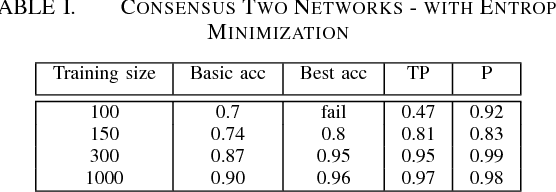
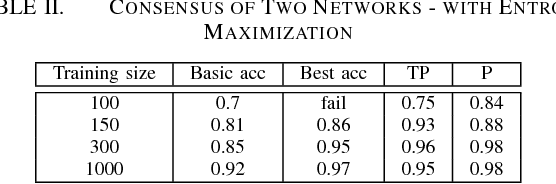
It is well known that for some tasks, labeled data sets may be hard to gather. Therefore, we wished to tackle here the problem of having insufficient training data. We examined learning methods from unlabeled data after an initial training on a limited labeled data set. The suggested approach can be used as an online learning method on the unlabeled test set. In the general classification task, whenever we predict a label with high enough confidence, we treat it as a true label and train the data accordingly. For the semantic segmentation task, a classic example for an expensive data labeling process, we do so pixel-wise. Our suggested approaches were applied on the MNIST data-set as a proof of concept for a vision classification task and on the ADE20K data-set in order to tackle the semi-supervised semantic segmentation problem.