Robust learning with the Hilbert-Schmidt independence criterion

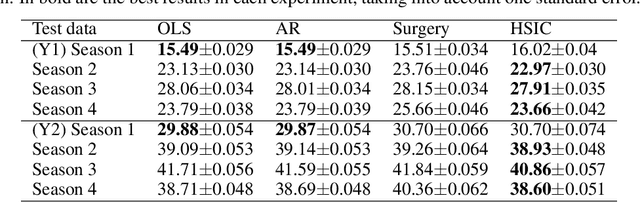
We investigate the use of a non-parametric independence measure, the Hilbert-Schmidt Independence Criterion (HSIC), as a loss-function for learning robust regression and classification models. This loss-function encourages learning models where the distribution of the residuals between the label and the model-prediction is statistically independent of the distribution of the instances themselves. This loss-function was first proposed by Mooij et al. [2009] in the context of learning causal graphs. We adapt it to the task of robust learning for unsupervised covariate shift: learning on a source domain without access to any instances or labels from the unknown target domain. We prove that the proposed loss is expected to generalize to a class of target domains described in terms of the complexity of their density ratio function with respect to the source domain. Experiments on tasks of unsupervised covariate shift demonstrate that models learned with the proposed loss-function outperform several baseline methods.