Fronthaul Quantization-Aware MU-MIMO Precoding for Sum Rate Maximization
Paper and Code
Jun 27, 2024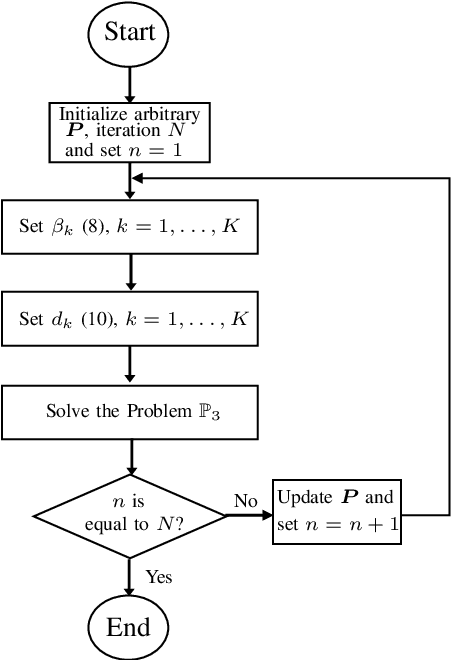
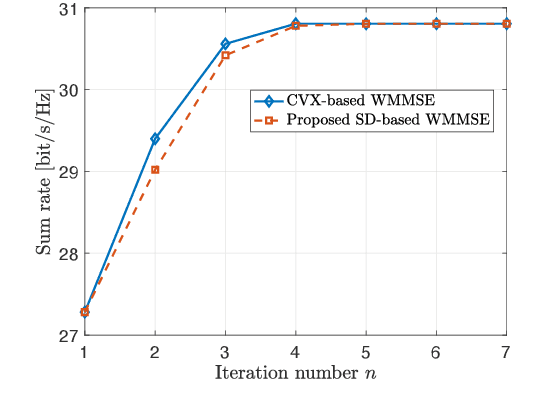
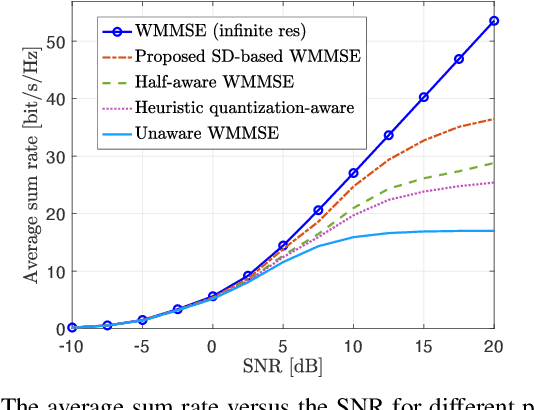
This paper considers a multi-user multiple-input multiple-output (MU-MIMO) system where the precoding matrix is selected in a baseband unit (BBU) and then sent over a digital fronthaul to the transmitting antenna array. The fronthaul has a limited bit resolution with a known quantization behavior. We formulate a new sum rate maximization problem where the precoding matrix elements must comply with the quantizer. We solve this non-convex mixed-integer problem to local optimality by a novel iterative algorithm inspired by the classical weighted minimum mean square error (WMMSE) approach. The precoding optimization subproblem becomes an integer least-squares problem, which we solve with a new algorithm using a sphere decoding (SD) approach. We show numerically that the proposed precoding technique vastly outperforms the baseline of optimizing an infinite-resolution precoder and then quantizing it. We also develop a heuristic quantization-aware precoding that outperforms the baseline while having comparable complexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge