Yasaman Khorsandmanesh
Channel-Coherence-Adaptive Two-Stage Fully Digital Combining for mmWave MIMO Systems
Aug 06, 2025Abstract:This paper considers a millimeter-wave wideband point-to-point MIMO system with fully digital transceivers at the base station and the user equipment (UE), focusing on mobile UE scenarios. A main challenge when building a digital UE combining is the large volume of baseband samples to handle. To mitigate computational and hardware complexity, we propose a novel two-stage digital combining scheme at the UE. The first stage reduces the $N_{\text{r}}$ received signals to $N_{\text{c}}$ streams before baseband processing, leveraging channel geometry for dimension reduction and updating at the beam coherence time, which is longer than the channel coherence time of the small-scale fading. By contrast, the second-stage combining is updated per fading realization. We develop a pilot-based channel estimation framework for this hardware setup based on maximum likelihoodestimation in both uplink and downlink. Digital precoding and combining designs are proposed, and a spectral efficiency expression that incorporates imperfect channel knowledge is derived. The numerical results demonstrate that the proposed approach outperforms hybrid beamforming, showcasing the attractiveness of using two-stage fully digital transceivers in future systems.
Fronthaul Quantization-Aware MU-MIMO Precoding for Sum Rate Maximization
Jun 27, 2024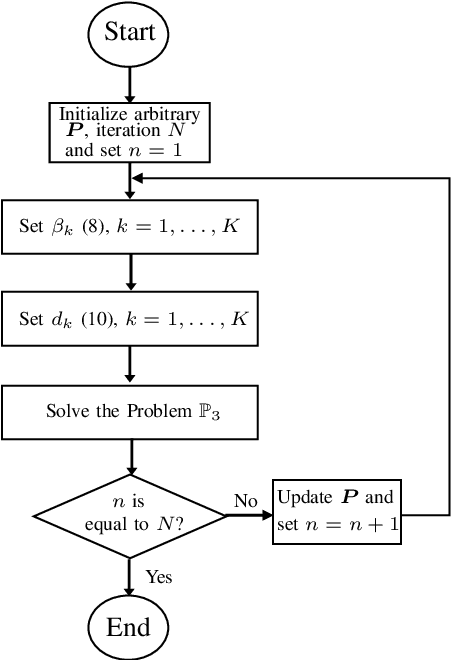
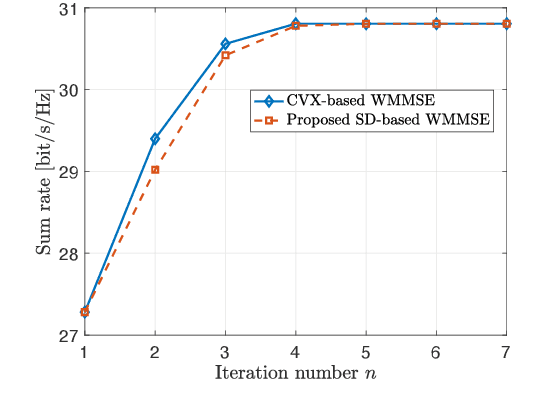
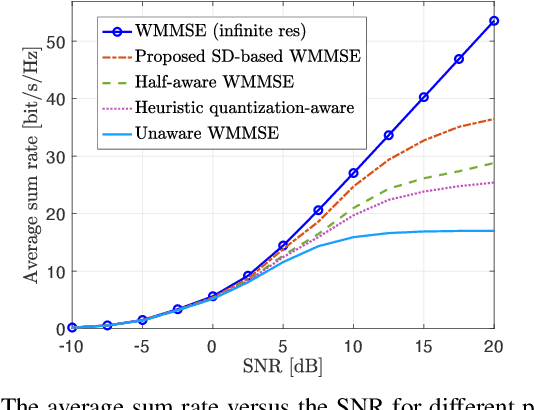
Abstract:This paper considers a multi-user multiple-input multiple-output (MU-MIMO) system where the precoding matrix is selected in a baseband unit (BBU) and then sent over a digital fronthaul to the transmitting antenna array. The fronthaul has a limited bit resolution with a known quantization behavior. We formulate a new sum rate maximization problem where the precoding matrix elements must comply with the quantizer. We solve this non-convex mixed-integer problem to local optimality by a novel iterative algorithm inspired by the classical weighted minimum mean square error (WMMSE) approach. The precoding optimization subproblem becomes an integer least-squares problem, which we solve with a new algorithm using a sphere decoding (SD) approach. We show numerically that the proposed precoding technique vastly outperforms the baseline of optimizing an infinite-resolution precoder and then quantizing it. We also develop a heuristic quantization-aware precoding that outperforms the baseline while having comparable complexity.
MSE Minimization in RIS-Aided MU-MIMO with Discrete Phase Shifts and Fronthaul Quantization
Jun 18, 2024Abstract:In this paper, we consider a downlink multi-user multiple-input multiple-output (MU-MIMO) communication assisted by a reconfigurable intelligent surface (RIS) and study the precoding and RIS configuration design under practical system constraints. These constraints include the limited-capacity fronthaul at the transmitter side and the finite resolution of RIS elements. We investigate the sum mean squared error (MSE) minimization problem and propose an algorithm based on the block coordinate descent method to optimize the precoding, RIS configuration, and receiver gains. We compute the precoding vectors and RIS configuration using the Schnorr-Euchner sphere decoding (SESD) method which delivers the optimal MSE-minimizing solution. We numerically evaluate the performance of the proposed SESD-based methods and corroborate their effectiveness in improving the system performance.
Joint Discrete Precoding and RIS Optimization for RIS-Assisted MU-MIMO Communication Systems
May 05, 2024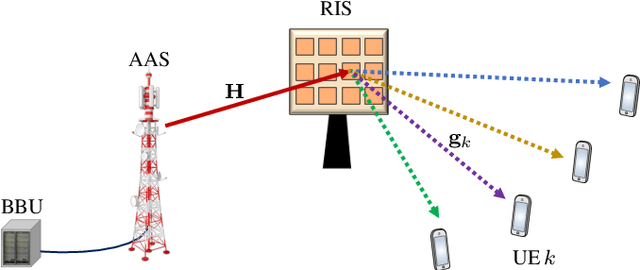
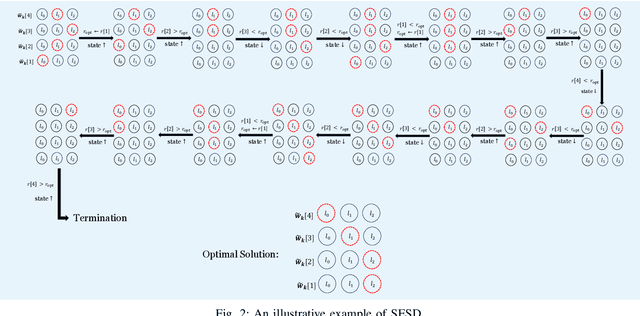
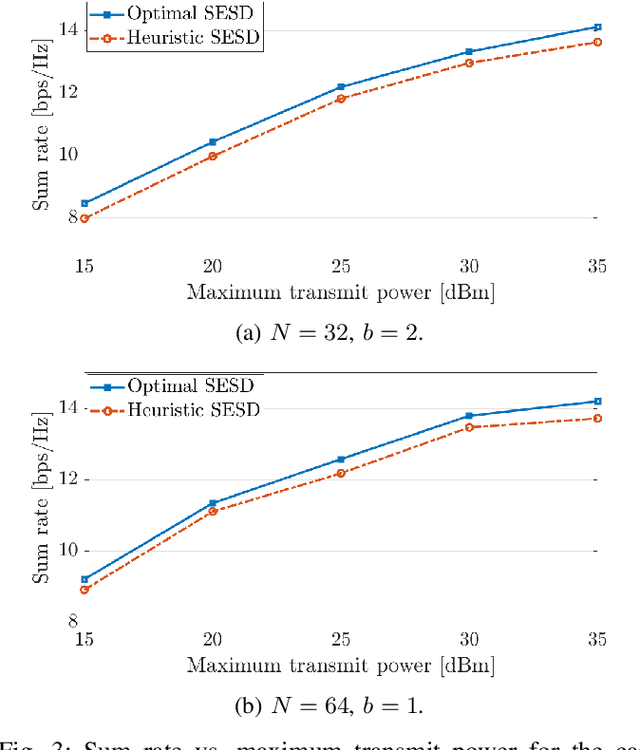
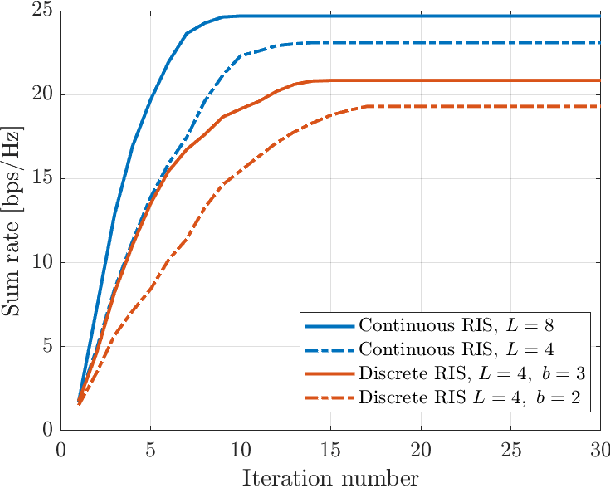
Abstract:This paper considers a multi-user multiple-input multiple-output (MU-MIMO) system where the downlink communication between a base station (BS) and multiple user equipments (UEs) is aided by a reconfigurable intelligent surface (RIS). We study the sum-rate maximization problem with the objective of finding the optimal precoding vectors and RIS configuration. Due to fronthaul limitation, each entry of the precoding vectors must be picked from a finite set of quantization labels. Furthermore, two scenarios for the RIS are investigated, one with continuous infinite-resolution reflection coefficients and another with discrete finite-resolution reflection coefficients. A novel framework is developed which, in contrast to the common literature that only offers sub-optimal solutions for optimization of discrete variables, is able to find the optimal solution to problems involving discrete constraints. Based on the classical weighted minimum mean square error (WMMSE), we transform the original problem into an equivalent weighted sum mean square error (MSE) minimization problem and solve it iteratively. We compute the optimal precoding vectors via an efficient algorithm inspired by sphere decoding (SD). For optimizing the discrete RIS configuration, two solutions based on the SD algorithm are developed: An optimal SD-based algorithm and a low-complexity heuristic method that can efficiently obtain RIS configuration without much loss in optimality. The effectiveness of the presented algorithms is corroborated via numerical simulations where it is shown that the proposed designs are remarkably superior to the commonly used benchmarks.
A Novel Discrete Phase Shift Design for RIS-Assisted Multi-User MIMO
Dec 09, 2023Abstract:Reconfigurable intelligent surface (RIS) is a newly-emerged technology that might fundamentally change how wireless networks are operated. Though extensively studied in recent years, the practical limitations of RIS are often neglected when assessing the performance of RIS-assisted communication networks. One of these limitations is that each RIS element is restricted to incur a controllable phase shift to the reflected signal from a predefined discrete set. This paper studies an RIS-assisted multi-user multiple-input multiple-output (MIMO) system, where an RIS with discrete phase shifts assists in simultaneous uplink data transmission from multiple user equipments (UEs) to a base station (BS). We aim to maximize the sum rate by optimizing the receive beamforming vectors and RIS phase shift configuration. To this end, we transform the original sum-rate maximization problem into a minimum mean square error (MMSE) minimization problem and employ the block coordinate descent (BCD) technique for iterative optimization of the variables until convergence. We formulate the discrete RIS phase shift optimization problem as a mixed-integer least squares problem and propose a novel method based on sphere decoding (SD) to solve it. Through numerical evaluation, we show that the proposed discrete phase shift design outperforms the conventional nearest point mapping method, which is prevalently used in previous works.
Optimized Precoding for MU-MIMO With Fronthaul Quantization
Sep 05, 2022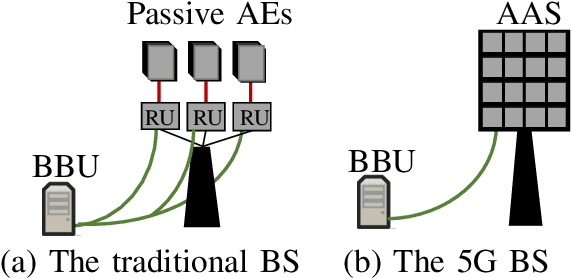
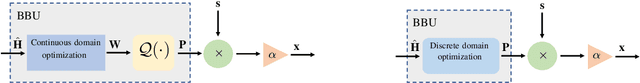
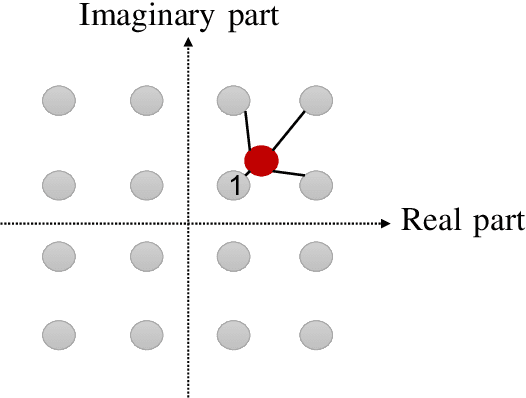
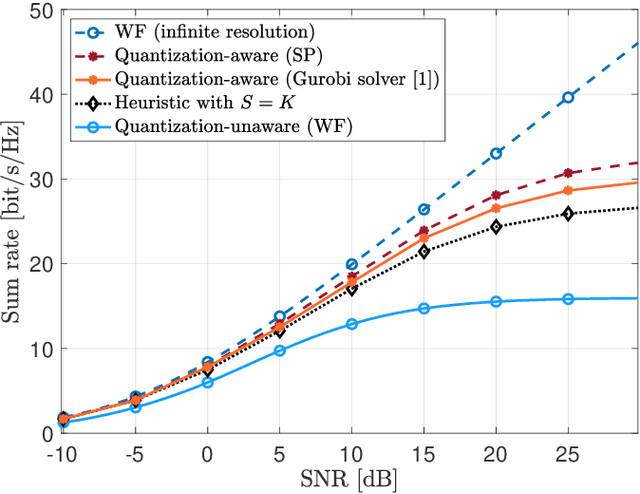
Abstract:One of the first widespread uses of multi-user multiple-input multiple-output (MU-MIMO) is in 5G networks, where each base station has an advanced antenna system (AAS) that is connected to the baseband unit (BBU) with a capacity-constrained fronthaul. In the AAS configuration, multiple passive antenna elements and radio units are integrated into a single box. This paper considers precoded downlink transmission over a single-cell MU-MIMO system. We study optimized linear precoding for AAS with a limited-capacity fronthaul, which requires the precoding matrix to be quantized. We propose a new precoding design that is aware of the fronthaul quantization and minimizes the mean-squared error at the receiver side. We compute the precoding matrix using a sphere decoding (SD) approach. We also propose a heuristic low-complexity approach to quantized precoding. This heuristic is computationally efficient enough for massive MIMO systems. The numerical results show that our proposed precoding significantly outperforms quantization-unaware precoding and other previous approaches in terms of the sum rate. The performance loss for our heuristic method compared to quantization-aware precoding is insignificant considering the complexity reduction, which makes the heuristic method feasible for real-time applications. We consider both perfect and imperfect channel state information.
Quantisation-aware Precoding for MU-MIMO with Limited-capacity Fronthaul
Feb 17, 2022


Abstract:Base stations in 5G and beyond use advanced antenna systems (AASs), where multiple passive antenna elements and radio units are integrated into a single box. A critical bottleneck of such a system is the digital fronthaul between the AAS and baseband unit (BBU), which has limited capacity. In this paper, we study an AAS used for precoded downlink transmission over a multi-user multiple-input multiple-output (MU-MIMO) channel. First, we present the baseline quantization-unaware precoding scheme created when a precoder is computed at the BBU and then quantized to be sent over the fronthaul. We propose a new precoding design that is aware of the fronthaul quantization. We formulate an optimization problem to minimize the mean squared error at the receiver side. We rewrite the problem to utilize mixed-integer programming to solve it. The numerical results manifest that our proposed precoding greatly outperforms quantization-unaware precoding in terms of sum rate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge