Joint Discrete Precoding and RIS Optimization for RIS-Assisted MU-MIMO Communication Systems
Paper and Code
May 05, 2024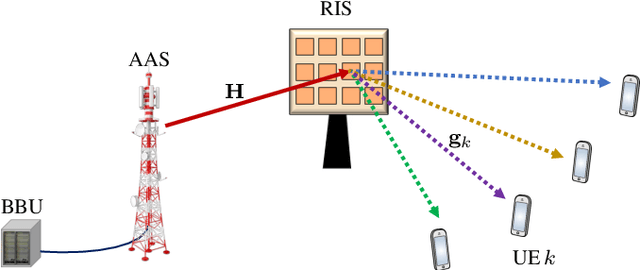
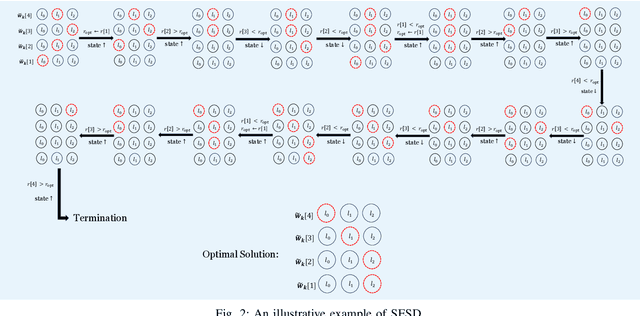
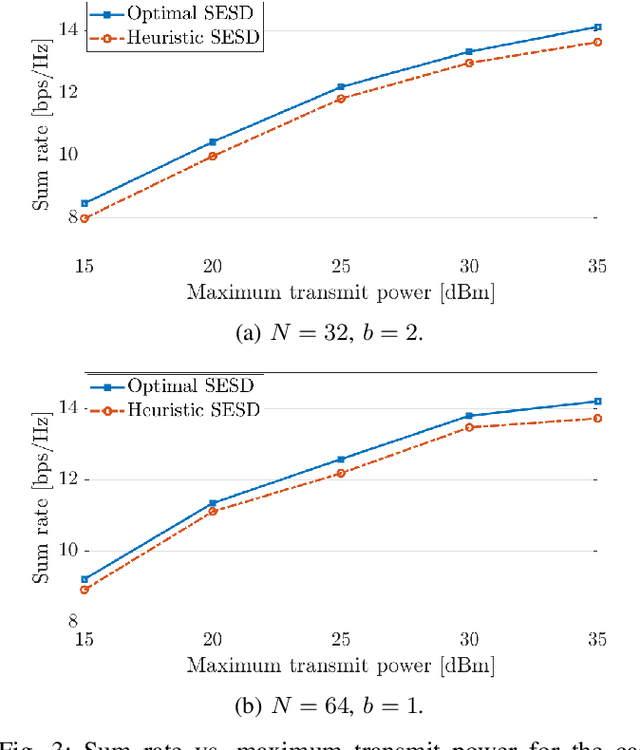
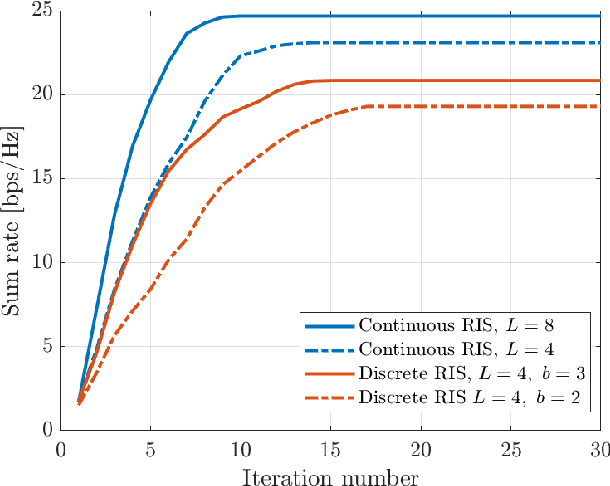
This paper considers a multi-user multiple-input multiple-output (MU-MIMO) system where the downlink communication between a base station (BS) and multiple user equipments (UEs) is aided by a reconfigurable intelligent surface (RIS). We study the sum-rate maximization problem with the objective of finding the optimal precoding vectors and RIS configuration. Due to fronthaul limitation, each entry of the precoding vectors must be picked from a finite set of quantization labels. Furthermore, two scenarios for the RIS are investigated, one with continuous infinite-resolution reflection coefficients and another with discrete finite-resolution reflection coefficients. A novel framework is developed which, in contrast to the common literature that only offers sub-optimal solutions for optimization of discrete variables, is able to find the optimal solution to problems involving discrete constraints. Based on the classical weighted minimum mean square error (WMMSE), we transform the original problem into an equivalent weighted sum mean square error (MSE) minimization problem and solve it iteratively. We compute the optimal precoding vectors via an efficient algorithm inspired by sphere decoding (SD). For optimizing the discrete RIS configuration, two solutions based on the SD algorithm are developed: An optimal SD-based algorithm and a low-complexity heuristic method that can efficiently obtain RIS configuration without much loss in optimality. The effectiveness of the presented algorithms is corroborated via numerical simulations where it is shown that the proposed designs are remarkably superior to the commonly used benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge