A matrix-inverse-free implementation of the MU-MIMO WMMSE beamforming algorithm

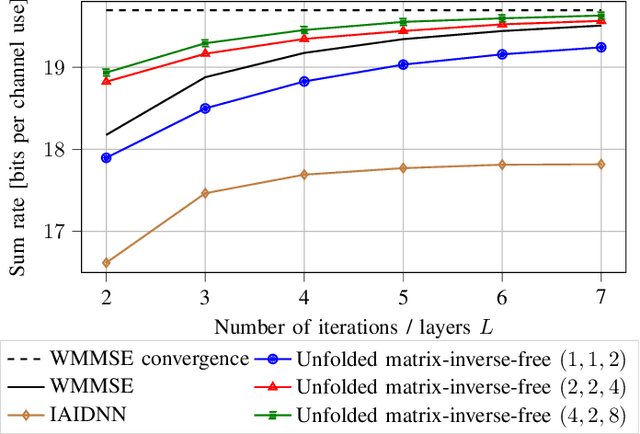
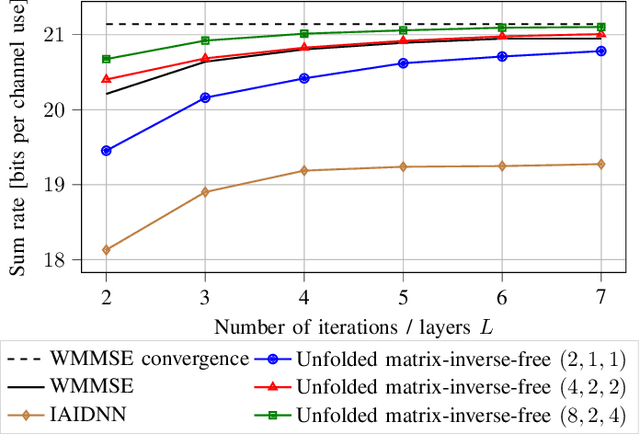
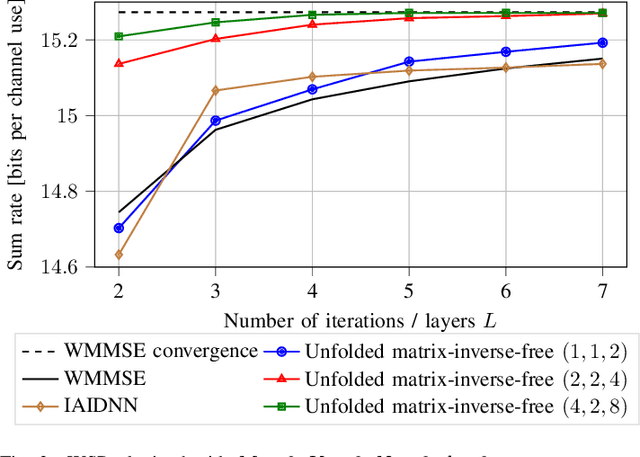
The WMMSE beamforming algorithm is a popular approach to address the NP-hard weighted sum rate (WSR) maximization beamforming problem. Although it efficiently finds a local optimum, it requires matrix inverses, eigendecompositions, and bisection searches, operations that are problematic for real-time implementation. In our previous work, we considered the MU-MISO case and effectively replaced such operations by resorting to a first-order method. Here, we consider the more general and challenging MU-MIMO case. Our earlier approach does not generalize to this scenario and cannot be applied to replace all the hard-to-parallelize operations that appear in the MU-MIMO case. Thus, we propose to leverage a reformulation of the auxiliary WMMSE function given by Hu et al. By applying gradient descent and Schulz iterations, we formulate the first variant of the WMMSE algorithm applicable to the MU-MIMO case that is free from matrix inverses and other serial operations and hence amenable to both real-time implementation and deep unfolding. From a theoretical viewpoint, we establish its convergence to a stationary point of the WSR maximization problem. From a practical viewpoint, we show that in a deep-unfolding-based implementation, the matrix-inverse-free WMMSE algorithm attains, within a fixed number of iterations, a WSR comparable to the original WMMSE algorithm truncated to the same number of iterations, yet with significant implementation advantages in terms of parallelizability and real-time execution.

Deep unfolding of the weighted MMSE beamforming algorithm

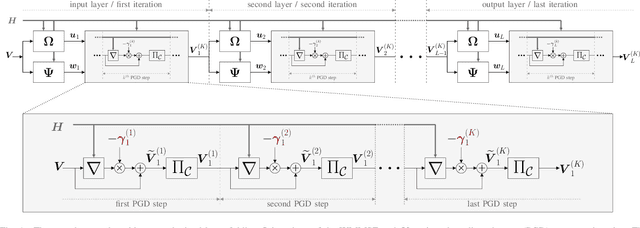
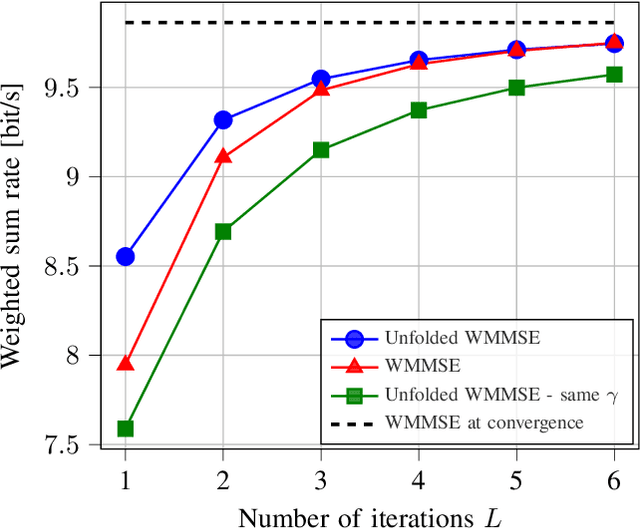
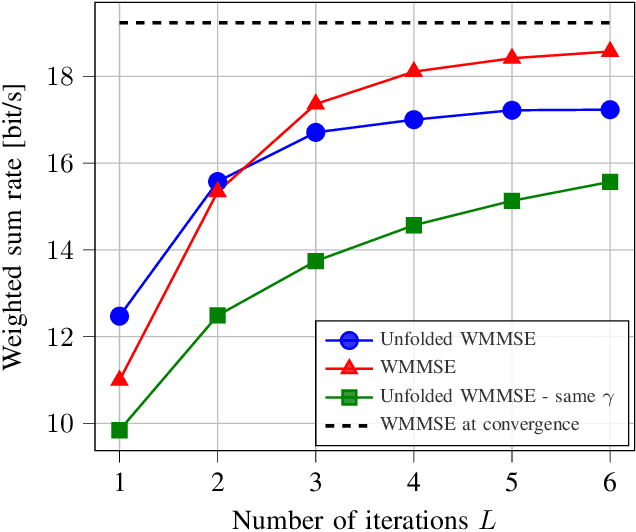
Downlink beamforming is a key technology for cellular networks. However, computing the transmit beamformer that maximizes the weighted sum rate subject to a power constraint is an NP-hard problem. As a result, iterative algorithms that converge to a local optimum are used in practice. Among them, the weighted minimum mean square error (WMMSE) algorithm has gained popularity, but its computational complexity and consequent latency has motivated the need for lower-complexity approximations at the expense of performance. Motivated by the recent success of deep unfolding in the trade-off between complexity and performance, we propose the novel application of deep unfolding to the WMMSE algorithm for a MISO downlink channel. The main idea consists of mapping a fixed number of iterations of the WMMSE algorithm into trainable neural network layers, whose architecture reflects the structure of the original algorithm. With respect to traditional end-to-end learning, deep unfolding naturally incorporates expert knowledge, with the benefits of immediate and well-grounded architecture selection, fewer trainable parameters, and better explainability. However, the formulation of the WMMSE algorithm, as described in Shi et al., is not amenable to be unfolded due to a matrix inversion, an eigendecomposition, and a bisection search performed at each iteration. Therefore, we present an alternative formulation that circumvents these operations by resorting to projected gradient descent. By means of simulations, we show that, in most of the settings, the unfolded WMMSE outperforms or performs equally to the WMMSE for a fixed number of iterations, with the advantage of a lower computational load.