A matrix-inverse-free implementation of the MU-MIMO WMMSE beamforming algorithm

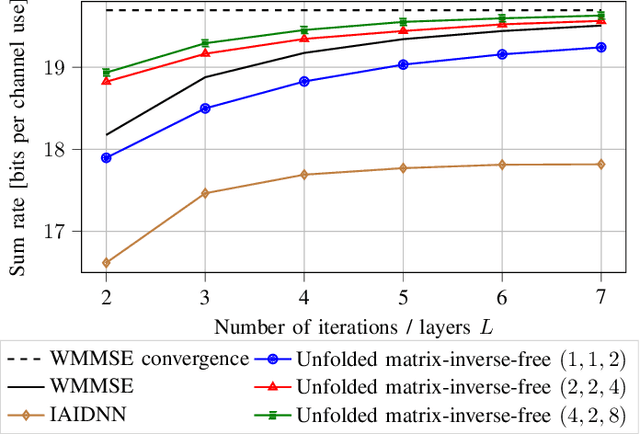
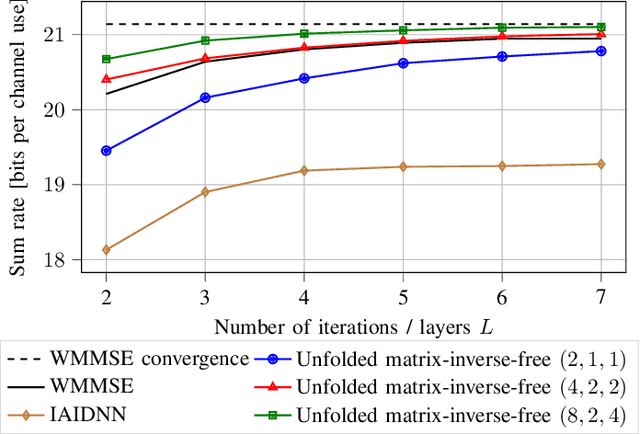
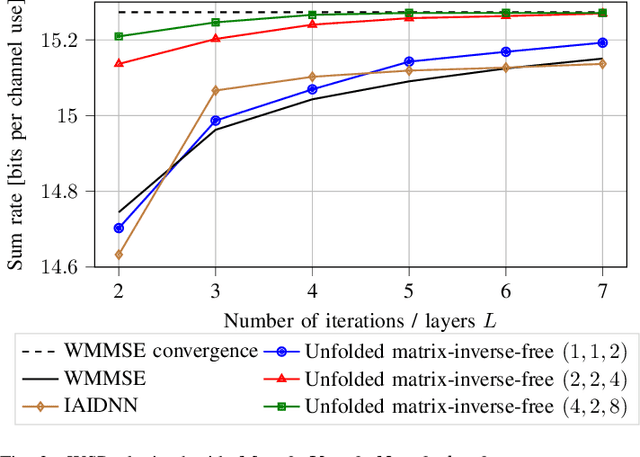
The WMMSE beamforming algorithm is a popular approach to address the NP-hard weighted sum rate (WSR) maximization beamforming problem. Although it efficiently finds a local optimum, it requires matrix inverses, eigendecompositions, and bisection searches, operations that are problematic for real-time implementation. In our previous work, we considered the MU-MISO case and effectively replaced such operations by resorting to a first-order method. Here, we consider the more general and challenging MU-MIMO case. Our earlier approach does not generalize to this scenario and cannot be applied to replace all the hard-to-parallelize operations that appear in the MU-MIMO case. Thus, we propose to leverage a reformulation of the auxiliary WMMSE function given by Hu et al. By applying gradient descent and Schulz iterations, we formulate the first variant of the WMMSE algorithm applicable to the MU-MIMO case that is free from matrix inverses and other serial operations and hence amenable to both real-time implementation and deep unfolding. From a theoretical viewpoint, we establish its convergence to a stationary point of the WSR maximization problem. From a practical viewpoint, we show that in a deep-unfolding-based implementation, the matrix-inverse-free WMMSE algorithm attains, within a fixed number of iterations, a WSR comparable to the original WMMSE algorithm truncated to the same number of iterations, yet with significant implementation advantages in terms of parallelizability and real-time execution.