Signal processing after quadratic random sketching with optical units

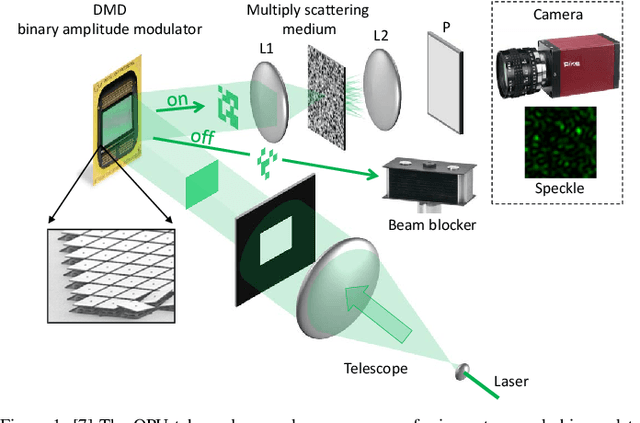
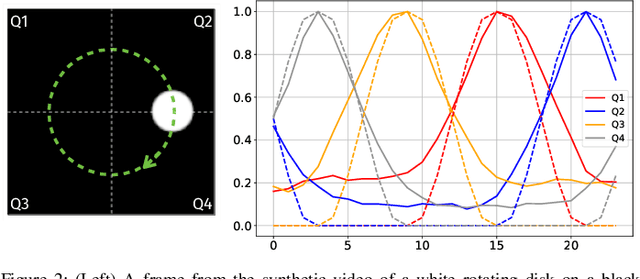
Random data sketching (or projection) is now a classical technique enabling, for instance, approximate numerical linear algebra and machine learning algorithms with reduced computational complexity and memory. In this context, the possibility of performing data processing (such as pattern detection or classification) directly in the sketched domain without accessing the original data was previously achieved for linear random sketching methods and compressive sensing. In this work, we show how to estimate simple signal processing tasks (such as deducing local variations in a image) directly using random quadratic projections achieved by an optical processing unit. The same approach allows for naive data classification methods directly operated in the sketched domain. We report several experiments confirming the power of our approach.

Signal processing with optical quadratic random sketches

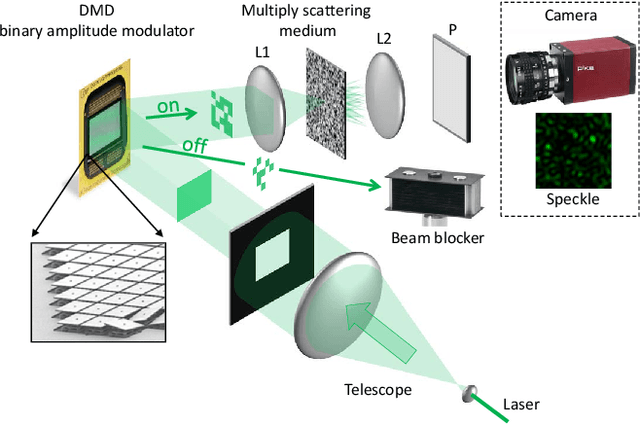
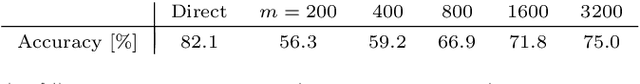
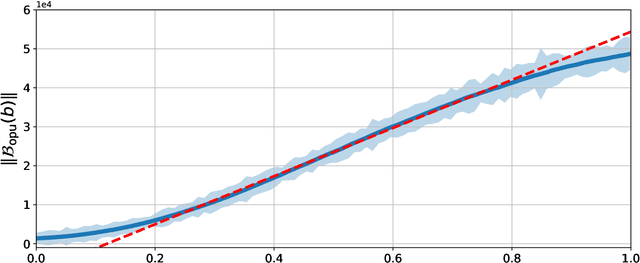
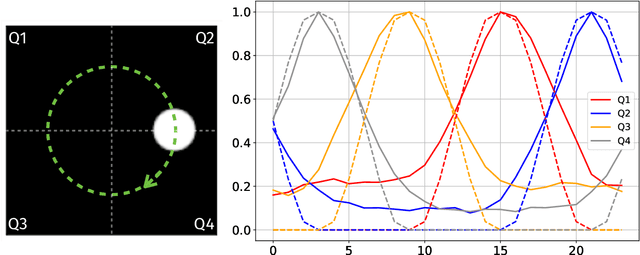
Random data sketching (or projection) is now a classical technique enabling, for instance, approximate numerical linear algebra and machine learning algorithms with reduced computational complexity and memory. In this context, the possibility of performing data processing (such as pattern detection or classification) directly in the sketched domain without accessing the original data was previously achieved for linear random sketching methods and compressive sensing. In this work, we show how to estimate simple signal processing tasks (such as deducing local variations in a image) directly using random quadratic projections achieved by an optical processing unit. The same approach allows for naive data classification methods directly operated in the sketched domain. We report several experiments confirming the power of our approach.

Photonic co-processors in HPC: using LightOn OPUs for Randomized Numerical Linear Algebra

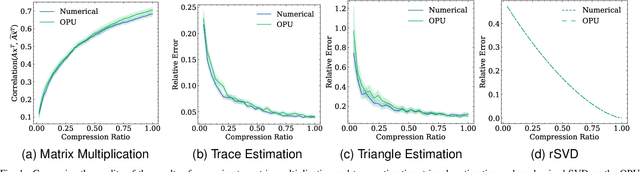
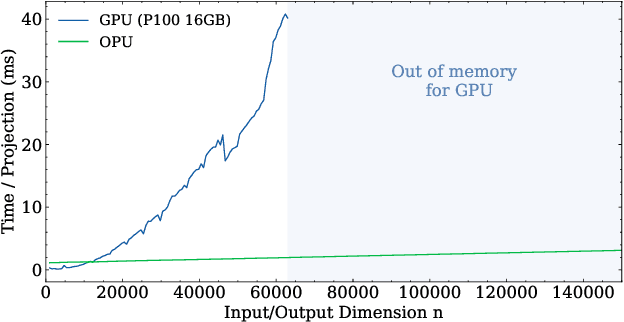
Randomized Numerical Linear Algebra (RandNLA) is a powerful class of methods, widely used in High Performance Computing (HPC). RandNLA provides approximate solutions to linear algebra functions applied to large signals, at reduced computational costs. However, the randomization step for dimensionality reduction may itself become the computational bottleneck on traditional hardware. Leveraging near constant-time linear random projections delivered by LightOn Optical Processing Units we show that randomization can be significantly accelerated, at negligible precision loss, in a wide range of important RandNLA algorithms, such as RandSVD or trace estimators.

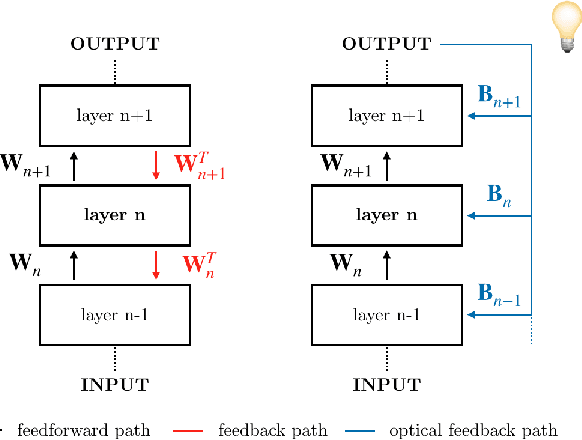
Hardware Beyond Backpropagation: a Photonic Co-Processor for Direct Feedback Alignment

The scaling hypothesis motivates the expansion of models past trillions of parameters as a path towards better performance. Recent significant developments, such as GPT-3, have been driven by this conjecture. However, as models scale-up, training them efficiently with backpropagation becomes difficult. Because model, pipeline, and data parallelism distribute parameters and gradients over compute nodes, communication is challenging to orchestrate: this is a bottleneck to further scaling. In this work, we argue that alternative training methods can mitigate these issues, and can inform the design of extreme-scale training hardware. Indeed, using a synaptically asymmetric method with a parallelizable backward pass, such as Direct Feedback Alignement, communication needs are drastically reduced. We present a photonic accelerator for Direct Feedback Alignment, able to compute random projections with trillions of parameters. We demonstrate our system on benchmark tasks, using both fully-connected and graph convolutional networks. Our hardware is the first architecture-agnostic photonic co-processor for training neural networks. This is a significant step towards building scalable hardware, able to go beyond backpropagation, and opening new avenues for deep learning.

Online Change Point Detection in Molecular Dynamics With Optical Random Features

Proteins are made of atoms constantly fluctuating, but can occasionally undergo large-scale changes. Such transitions are of biological interest, linking the structure of a protein to its function with a cell. Atomic-level simulations, such as Molecular Dynamics (MD), are used to study these events. However, molecular dynamics simulations produce time series with multiple observables, while changes often only affect a few of them. Therefore, detecting conformational changes has proven to be challenging for most change-point detection algorithms. In this work, we focus on the identification of such events given many noisy observables. In particular, we show that the No-prior-Knowledge Exponential Weighted Moving Average (NEWMA) algorithm can be used along optical hardware to successfully identify these changes in real-time. Our method does not need to distinguish between the background of a protein and the protein itself. For larger simulations, it is faster than using traditional silicon hardware and has a lower memory footprint. This technique may enhance the sampling of the conformational space of molecules. It may also be used to detect change-points in other sequential data with a large number of features.

Light-in-the-loop: using a photonics co-processor for scalable training of neural networks

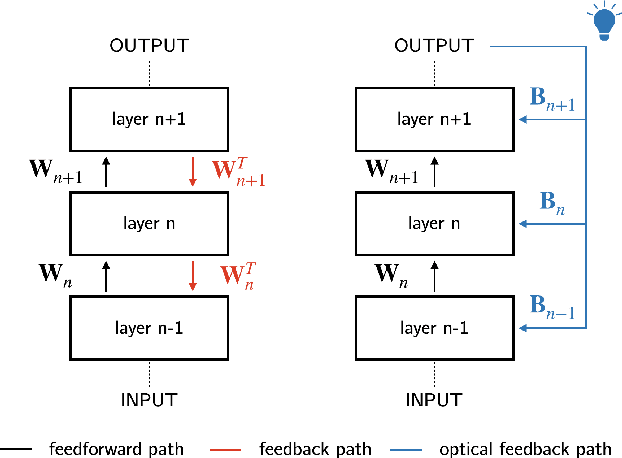
As neural networks grow larger and more complex and data-hungry, training costs are skyrocketing. Especially when lifelong learning is necessary, such as in recommender systems or self-driving cars, this might soon become unsustainable. In this study, we present the first optical co-processor able to accelerate the training phase of digitally-implemented neural networks. We rely on direct feedback alignment as an alternative to backpropagation, and perform the error projection step optically. Leveraging the optical random projections delivered by our co-processor, we demonstrate its use to train a neural network for handwritten digits recognition.

Kernel computations from large-scale random features obtained by Optical Processing Units

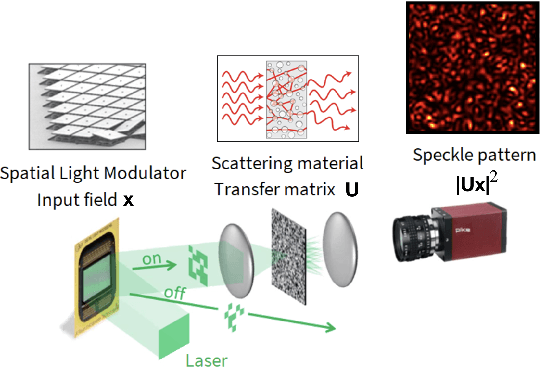
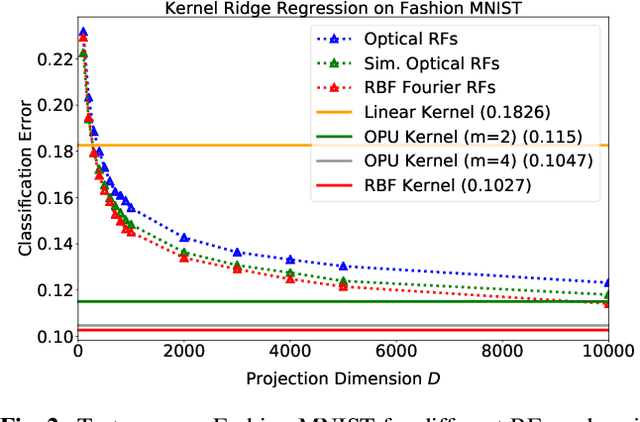
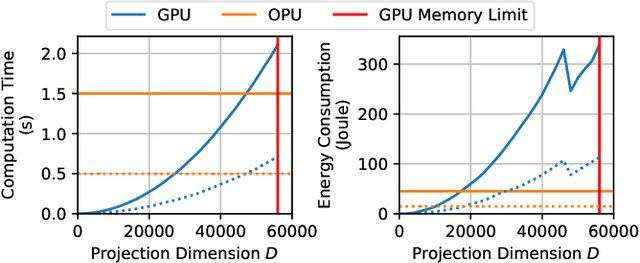
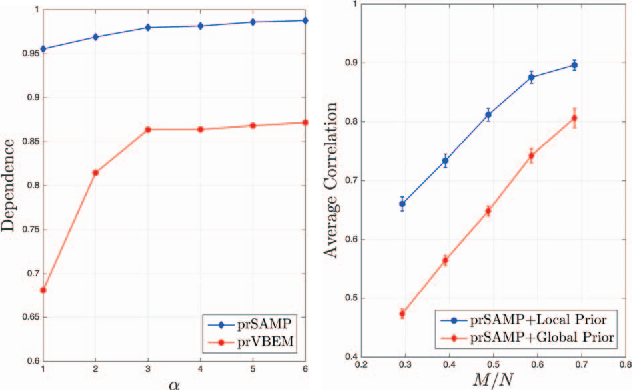
Approximating kernel functions with random features (RFs)has been a successful application of random projections for nonparametric estimation. However, performing random projections presents computational challenges for large-scale problems. Recently, a new optical hardware called Optical Processing Unit (OPU) has been developed for fast and energy-efficient computation of large-scale RFs in the analog domain. More specifically, the OPU performs the multiplication of input vectors by a large random matrix with complex-valued i.i.d. Gaussian entries, followed by the application of an element-wise squared absolute value operation - this last nonlinearity being intrinsic to the sensing process. In this paper, we show that this operation results in a dot-product kernel that has connections to the polynomial kernel, and we extend this computation to arbitrary powers of the feature map. Experiments demonstrate that the OPU kernel and its RF approximation achieve competitive performance in applications using kernel ridge regression and transfer learning for image classification. Crucially, thanks to the use of the OPU, these results are obtained with time and energy savings.

Don't take it lightly: Phasing optical random projections with unknown operators

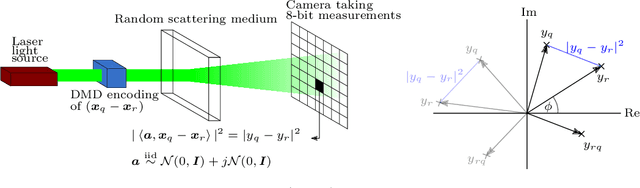
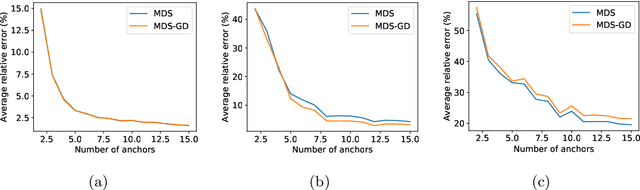
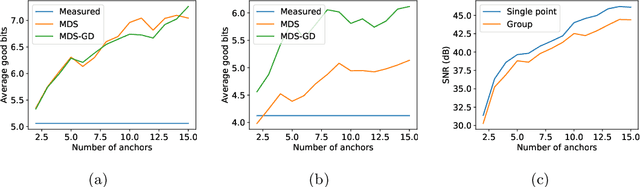
In this paper we tackle the problem of recovering the phase of complex linear measurements when only magnitude information is available and we control the input. We are motivated by the recent development of dedicated optics-based hardware for rapid random projections which leverages the propagation of light in random media. A signal of interest $\mathbf{\xi} \in \mathbb{R}^N$ is mixed by a random scattering medium to compute the projection $\mathbf{y} = \mathbf{A} \mathbf{\xi}$, with $\mathbf{A} \in \mathbb{C}^{M \times N}$ being a realization of a standard complex Gaussian iid random matrix. Two difficulties arise in this scheme: only the intensity ${|\mathbf{y}|}^2$ can be recorded by the camera, and the transmission matrix $\mathbf{A}$ is unknown. We show that even without knowing $\mathbf{A}$, we can recover the unknown phase of $\mathbf{y}$ for some equivalent transmission matrix with the same distribution as $\mathbf{A}$. Our method is based on two observations: first, changing the phase of any row of $\mathbf{A}$ does not change its distribution; and second, since we control the input we can interfere $\mathbf{\xi}$ with arbitrary reference signals. We show how to leverage these observations to cast the measurement phase retrieval problem as a Euclidean distance geometry problem. We demonstrate appealing properties of the proposed algorithm on both numerical simulations and in real hardware experiments. Not only does our algorithm accurately recover the missing phase, but it mitigates the effects of quantization and the sensitivity threshold, thus also improving the measured magnitudes.

Intensity-only optical compressive imaging using a multiply scattering material and a double phase retrieval approach

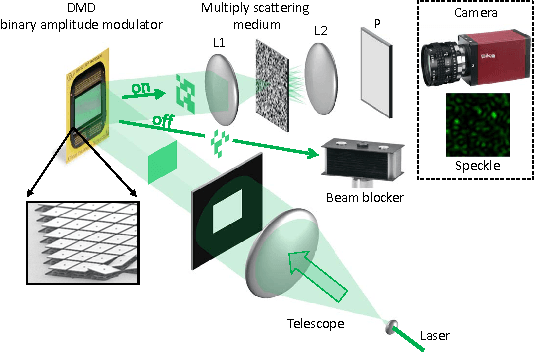
In this paper, the problem of compressive imaging is addressed using natural randomization by means of a multiply scattering medium. To utilize the medium in this way, its corresponding transmission matrix must be estimated. To calibrate the imager, we use a digital micromirror device (DMD) as a simple, cheap, and high-resolution binary intensity modulator. We propose a phase retrieval algorithm which is well adapted to intensity-only measurements on the camera, and to the input binary intensity patterns, both to estimate the complex transmission matrix as well as image reconstruction. We demonstrate promising experimental results for the proposed algorithm using the MNIST dataset of handwritten digits as example images.

Random Projections through multiple optical scattering: Approximating kernels at the speed of light

Random projections have proven extremely useful in many signal processing and machine learning applications. However, they often require either to store a very large random matrix, or to use a different, structured matrix to reduce the computational and memory costs. Here, we overcome this difficulty by proposing an analog, optical device, that performs the random projections literally at the speed of light without having to store any matrix in memory. This is achieved using the physical properties of multiple coherent scattering of coherent light in random media. We use this device on a simple task of classification with a kernel machine, and we show that, on the MNIST database, the experimental results closely match the theoretical performance of the corresponding kernel. This framework can help make kernel methods practical for applications that have large training sets and/or require real-time prediction. We discuss possible extensions of the method in terms of a class of kernels, speed, memory consumption and different problems.