Learning sparse structures for physics-inspired compressed sensing

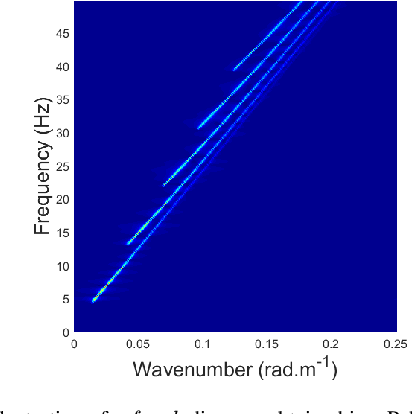
In underwater acoustics, shallow water environments act as modal dispersive waveguides when considering low-frequency sources. In this context, propagating signals can be described as a sum of few modal components, each of them propagating according to its own wavenumber. Estimating these wavenumbers is of key interest to understand the propagating environment as well as the emitting source. To solve this problem, we proposed recently a Bayesian approach exploiting a sparsity-inforcing prior. When dealing with broadband sources, this model can be further improved by integrating the particular dependence linking the wavenumbers from one frequency to the other. In this contribution, we propose to resort to a new approach relying on a restricted Boltzmann machine, exploited as a generic structured sparsity-inforcing model. This model, derived from deep Bayesian networks, can indeed be efficiently learned on physically realistic simulated data using well-known and proven algorithms.

An Efficient Algorithm for Video Super-Resolution Based On a Sequential Model

In this work, we propose a novel procedure for video super-resolution, that is the recovery of a sequence of high-resolution images from its low-resolution counterpart. Our approach is based on a "sequential" model (i.e., each high-resolution frame is supposed to be a displaced version of the preceding one) and considers the use of sparsity-enforcing priors. Both the recovery of the high-resolution images and the motion fields relating them is tackled. This leads to a large-dimensional, non-convex and non-smooth problem. We propose an algorithmic framework to address the latter. Our approach relies on fast gradient evaluation methods and modern optimization techniques for non-differentiable/non-convex problems. Unlike some other previous works, we show that there exists a provably-convergent method with a complexity linear in the problem dimensions. We assess the proposed optimization method on {several video benchmarks and emphasize its good performance with respect to the state of the art.}

Approximate Message Passing with Restricted Boltzmann Machine Priors

Approximate Message Passing (AMP) has been shown to be an excellent statistical approach to signal inference and compressed sensing problem. The AMP framework provides modularity in the choice of signal prior; here we propose a hierarchical form of the Gauss-Bernouilli prior which utilizes a Restricted Boltzmann Machine (RBM) trained on the signal support to push reconstruction performance beyond that of simple iid priors for signals whose support can be well represented by a trained binary RBM. We present and analyze two methods of RBM factorization and demonstrate how these affect signal reconstruction performance within our proposed algorithm. Finally, using the MNIST handwritten digit dataset, we show experimentally that using an RBM allows AMP to approach oracle-support performance.

Random Projections through multiple optical scattering: Approximating kernels at the speed of light

Random projections have proven extremely useful in many signal processing and machine learning applications. However, they often require either to store a very large random matrix, or to use a different, structured matrix to reduce the computational and memory costs. Here, we overcome this difficulty by proposing an analog, optical device, that performs the random projections literally at the speed of light without having to store any matrix in memory. This is achieved using the physical properties of multiple coherent scattering of coherent light in random media. We use this device on a simple task of classification with a kernel machine, and we show that, on the MNIST database, the experimental results closely match the theoretical performance of the corresponding kernel. This framework can help make kernel methods practical for applications that have large training sets and/or require real-time prediction. We discuss possible extensions of the method in terms of a class of kernels, speed, memory consumption and different problems.

Statistical inference with probabilistic graphical models

These are notes from the lecture of Devavrat Shah given at the autumn school "Statistical Physics, Optimization, Inference, and Message-Passing Algorithms", that took place in Les Houches, France from Monday September 30th, 2013, till Friday October 11th, 2013. The school was organized by Florent Krzakala from UPMC & ENS Paris, Federico Ricci-Tersenghi from La Sapienza Roma, Lenka Zdeborova from CEA Saclay & CNRS, and Riccardo Zecchina from Politecnico Torino. This lecture of Devavrat Shah (MIT) covers the basics of inference and learning. It explains how inference problems are represented within structures known as graphical models. The theoretical basis of the belief propagation algorithm is then explained and derived. This lecture sets the stage for generalizations and applications of message passing algorithms.