Uncertainty of Atmospheric Motion Vectors by Sampling Tempered Posterior Distributions

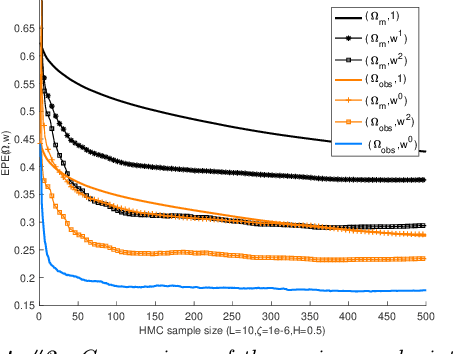
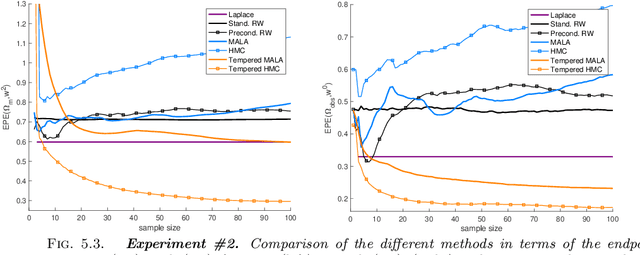
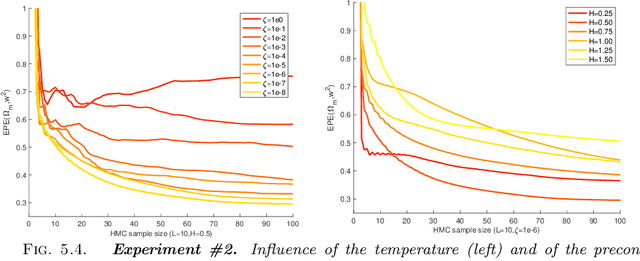
Atmospheric motion vectors (AMVs) extracted from satellite imagery are the only wind observations with good global coverage. They are important features for feeding numerical weather prediction (NWP) models. Several Bayesian models have been proposed to estimate AMVs. Although critical for correct assimilation into NWP models, very few methods provide a thorough characterization of the estimation errors. The difficulty of estimating errors stems from the specificity of the posterior distribution, which is both very high dimensional, and highly ill-conditioned due to a singular likelihood, which becomes critical in particular in the case of missing data (unobserved pixels). This work studies the evaluation of the expected error of AMVs using gradient-based Markov Chain Monte Carlo (MCMC) algorithms. Our main contribution is to propose a tempering strategy, which amounts to sampling a local approximation of the joint posterior distribution of AMVs and image variables in the neighborhood of a point estimate. In addition, we provide efficient preconditioning with the covariance related to the prior family itself (fractional Brownian motion), with possibly different hyper-parameters. From a theoretical point of view, we show that under regularity assumptions, the family of tempered posterior distributions converges in distribution as temperature decreases to an {optimal} Gaussian approximation at a point estimate given by the Maximum A Posteriori (MAP) log-density. From an empirical perspective, we evaluate the proposed approach based on some quantitative Bayesian evaluation criteria. Our numerical simulations performed on synthetic and real meteorological data reveal a significant gain in terms of accuracy of the AMV point estimates and of their associated expected error estimates, but also a substantial acceleration in the convergence speed of the MCMC algorithms.

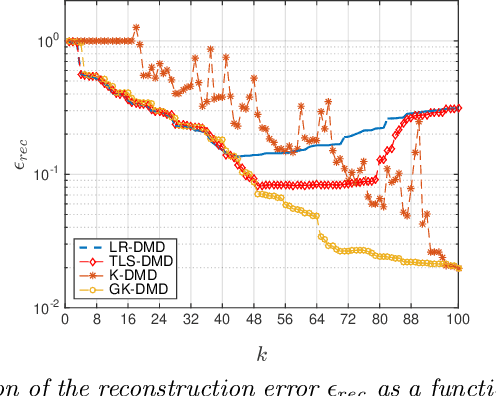
Optimal Low-Rank Dynamic Mode Decomposition

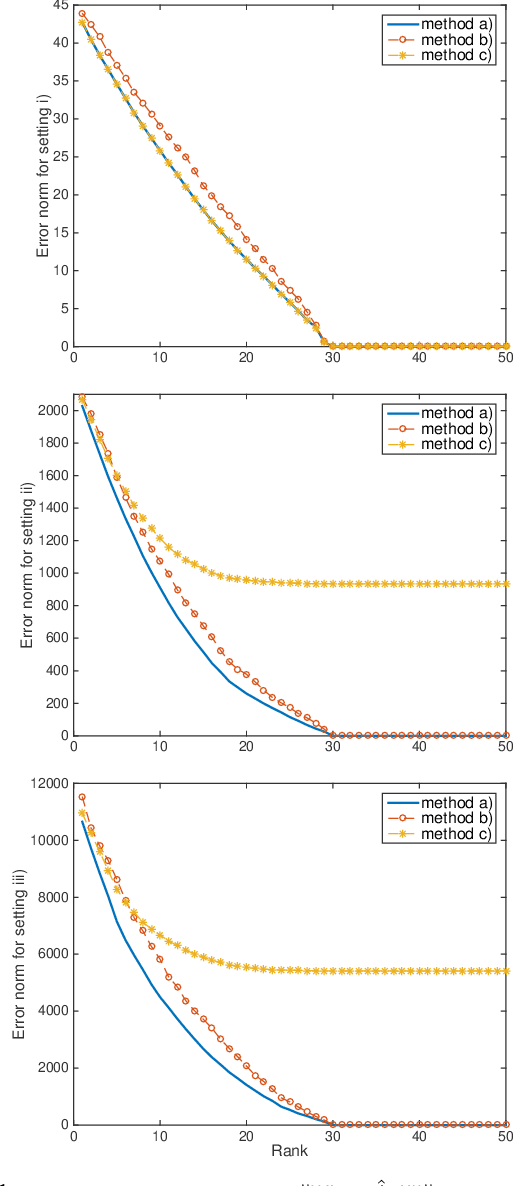
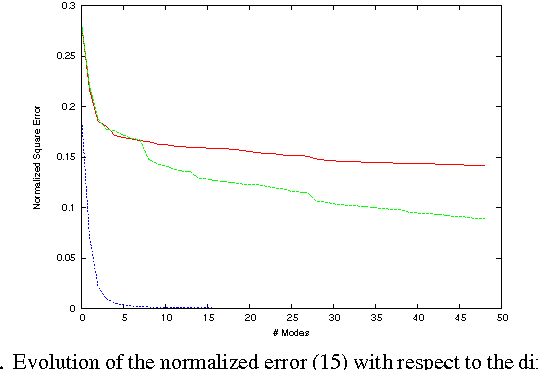
Dynamic Mode Decomposition (DMD) has emerged as a powerful tool for analyzing the dynamics of non-linear systems from experimental datasets. Recently, several attempts have extended DMD to the context of low-rank approximations. This extension is of particular interest for reduced-order modeling in various applicative domains, e.g. for climate prediction, to study molecular dynamics or micro-electromechanical devices. This low-rank extension takes the form of a non-convex optimization problem. To the best of our knowledge, only sub-optimal algorithms have been proposed in the literature to compute the solution of this problem. In this paper, we prove that there exists a closed-form optimal solution to this problem and design an effective algorithm to compute it based on Singular Value Decomposition (SVD). A toy-example illustrates the gain in performance of the proposed algorithm compared to state-of-the-art techniques.

Reduced-Order Modeling Of Hidden Dynamics

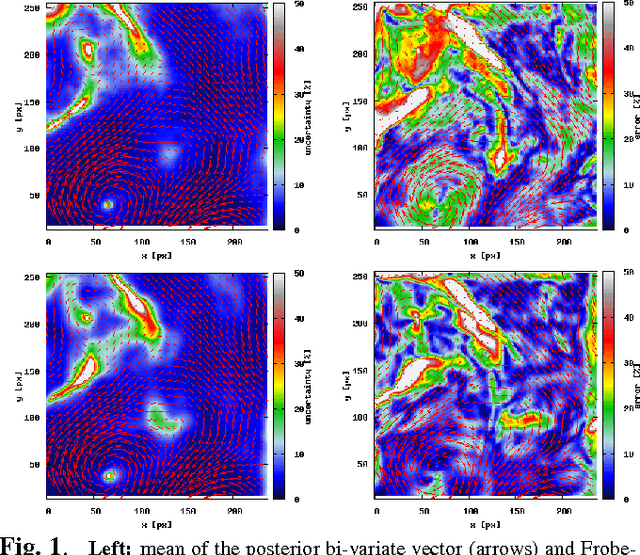
The objective of this paper is to investigate how noisy and incomplete observations can be integrated in the process of building a reduced-order model. This problematic arises in many scientific domains where there exists a need for accurate low-order descriptions of highly-complex phenomena, which can not be directly and/or deterministically observed. Within this context, the paper proposes a probabilistic framework for the construction of "POD-Galerkin" reduced-order models. Assuming a hidden Markov chain, the inference integrates the uncertainty of the hidden states relying on their posterior distribution. Simulations show the benefits obtained by exploiting the proposed framework.

Optimal Kernel-Based Dynamic Mode Decomposition

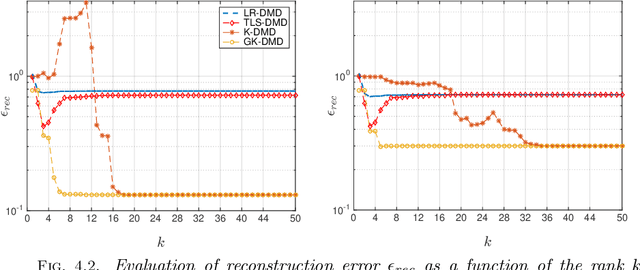
The state-of-the-art algorithm known as kernel-based dynamic mode decomposition (K-DMD) provides a sub-optimal solution to the problem of reduced modeling of a dynamical system based on a finite approximation of the Koopman operator. It relies on crude approximations and on restrictive assumptions. The purpose of this work is to propose a kernel-based algorithm solving exactly this low-rank approximation problem in a general setting.

Low-Rank Dynamic Mode Decomposition: Optimal Solution in Polynomial-Time

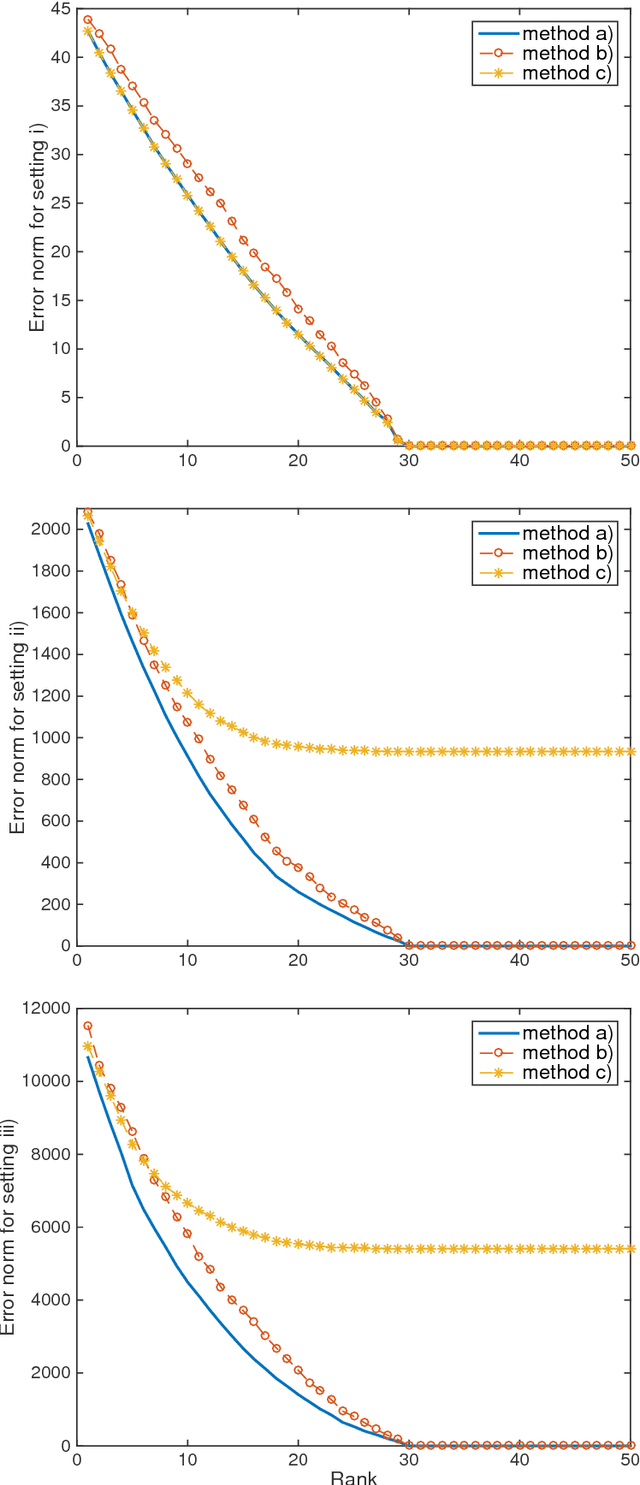
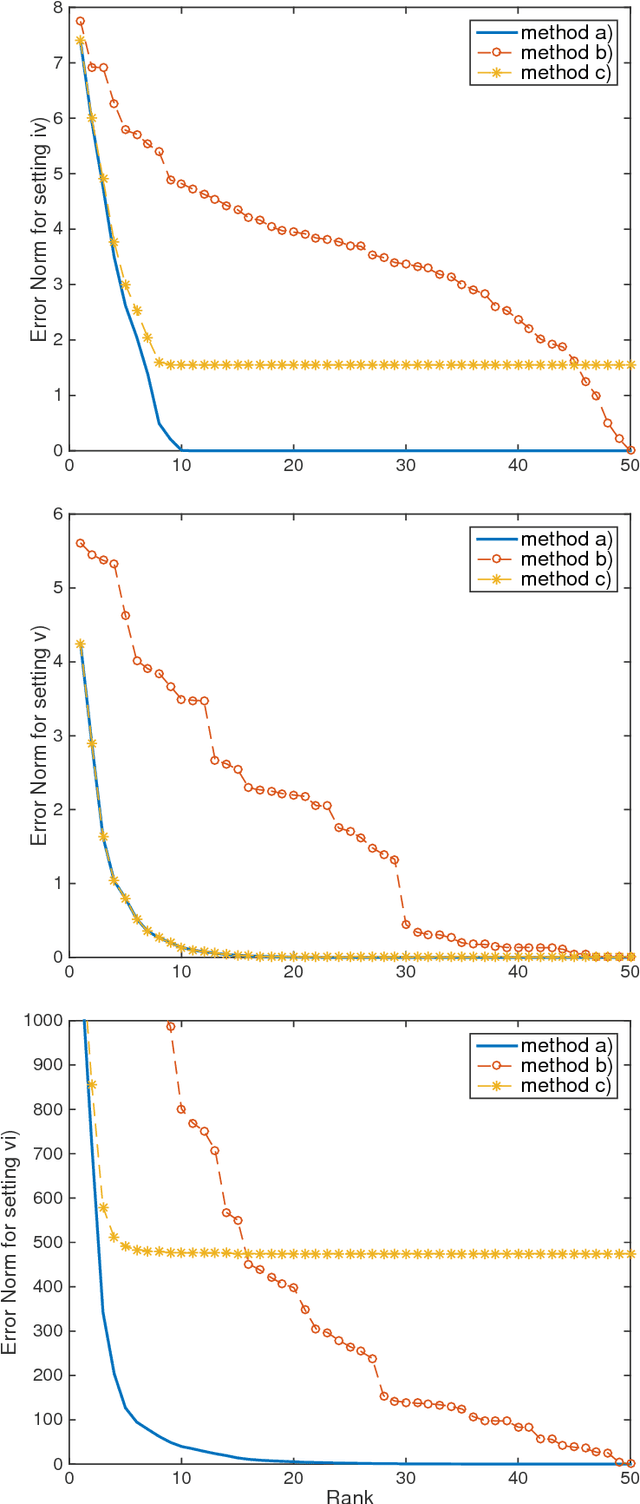
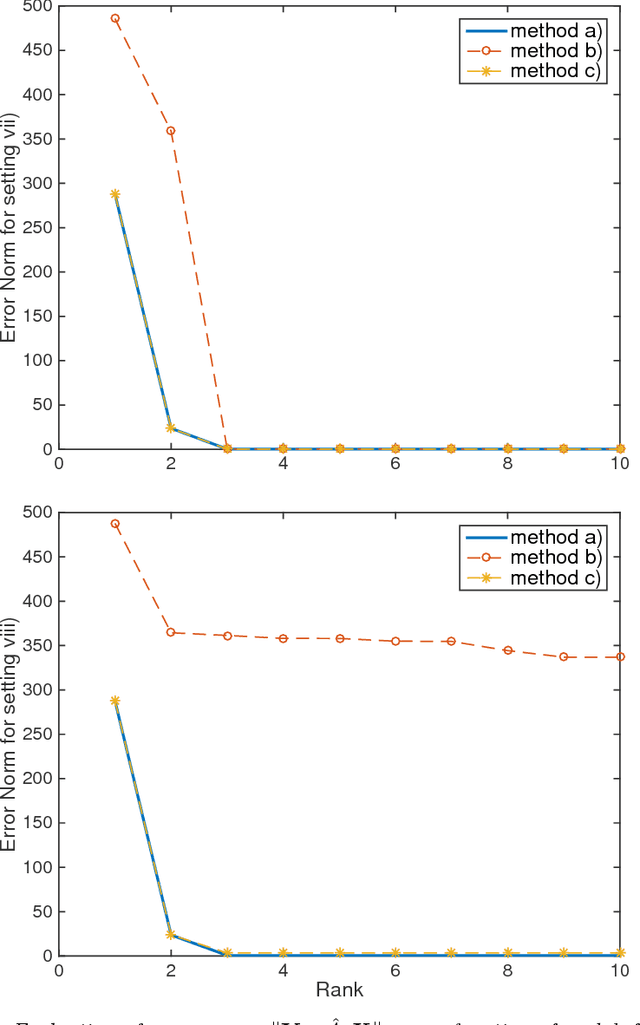
This work studies the linear approximation of high-dimensional dynamical systems using low-rank dynamic mode decomposition (DMD). Searching this approximation in a data-driven approach can be formalised as attempting to solve a low-rank constrained optimisation problem. This problem is non-convex and state-of-the-art algorithms are all sub-optimal. This paper shows that there exists a closed-form solution, which can be computed in polynomial-time, and characterises the $\ell_2$-norm of the optimal approximation error. The theoretical results serve to design low-complexity algorithms building reduced models from the optimal solution, based on singular value decomposition or low-rank DMD. The algorithms are evaluated by numerical simulations using synthetic and physical data benchmarks.

An Efficient Algorithm for Video Super-Resolution Based On a Sequential Model

In this work, we propose a novel procedure for video super-resolution, that is the recovery of a sequence of high-resolution images from its low-resolution counterpart. Our approach is based on a "sequential" model (i.e., each high-resolution frame is supposed to be a displaced version of the preceding one) and considers the use of sparsity-enforcing priors. Both the recovery of the high-resolution images and the motion fields relating them is tackled. This leads to a large-dimensional, non-convex and non-smooth problem. We propose an algorithmic framework to address the latter. Our approach relies on fast gradient evaluation methods and modern optimization techniques for non-differentiable/non-convex problems. Unlike some other previous works, we show that there exists a provably-convergent method with a complexity linear in the problem dimensions. We assess the proposed optimization method on {several video benchmarks and emphasize its good performance with respect to the state of the art.}

Self-similar prior and wavelet bases for hidden incompressible turbulent motion

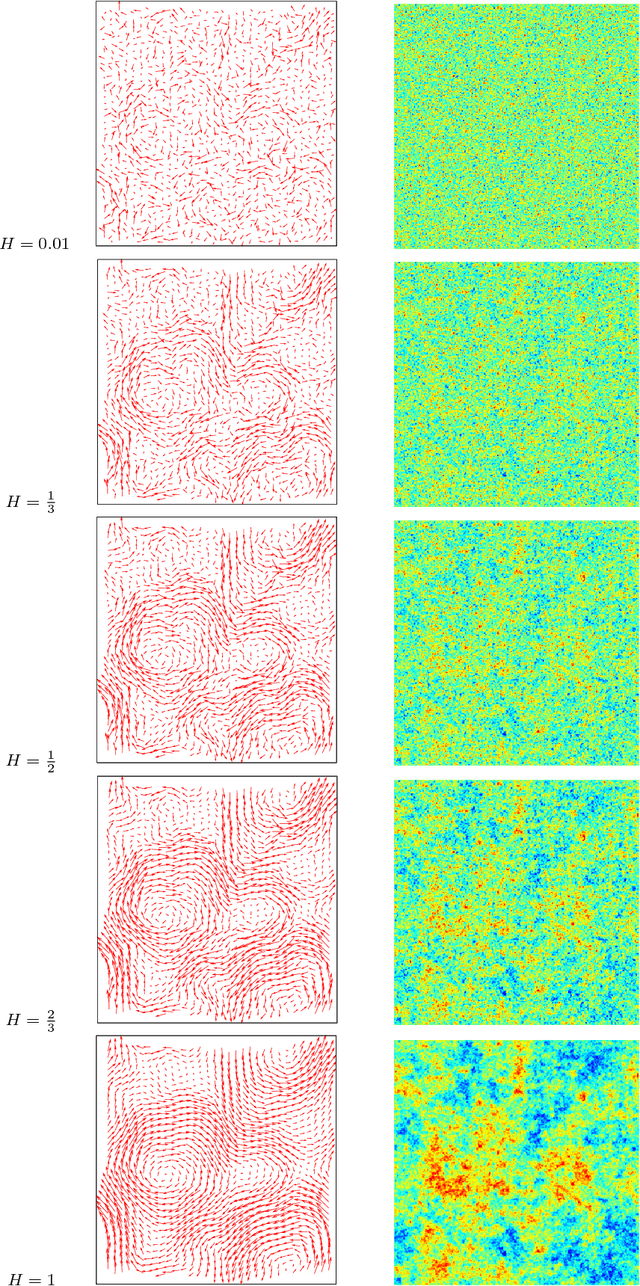
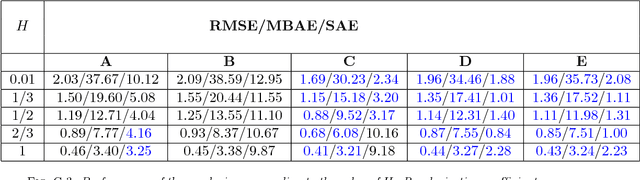
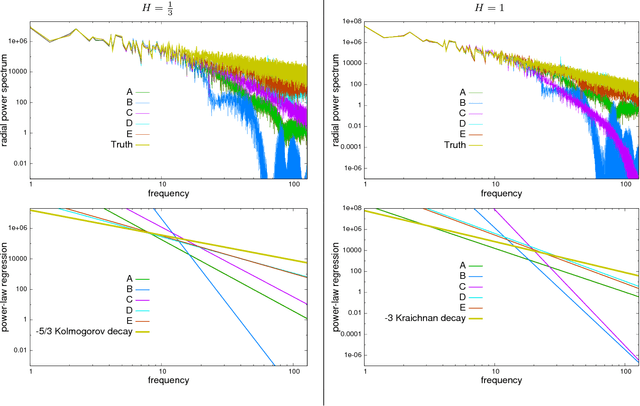
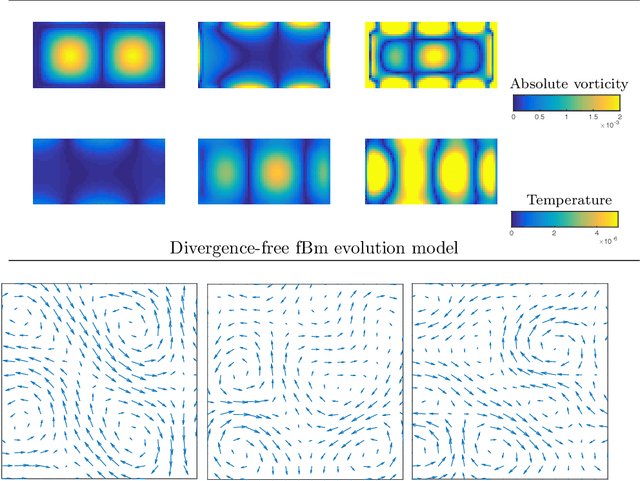
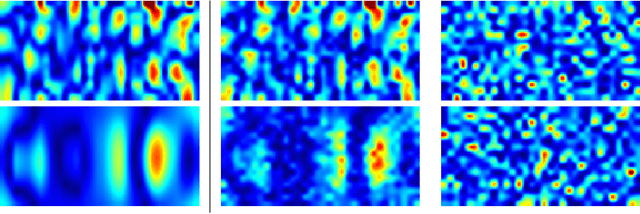
This work is concerned with the ill-posed inverse problem of estimating turbulent flows from the observation of an image sequence. From a Bayesian perspective, a divergence-free isotropic fractional Brownian motion (fBm) is chosen as a prior model for instantaneous turbulent velocity fields. This self-similar prior characterizes accurately second-order statistics of velocity fields in incompressible isotropic turbulence. Nevertheless, the associated maximum a posteriori involves a fractional Laplacian operator which is delicate to implement in practice. To deal with this issue, we propose to decompose the divergent-free fBm on well-chosen wavelet bases. As a first alternative, we propose to design wavelets as whitening filters. We show that these filters are fractional Laplacian wavelets composed with the Leray projector. As a second alternative, we use a divergence-free wavelet basis, which takes implicitly into account the incompressibility constraint arising from physics. Although the latter decomposition involves correlated wavelet coefficients, we are able to handle this dependence in practice. Based on these two wavelet decompositions, we finally provide effective and efficient algorithms to approach the maximum a posteriori. An intensive numerical evaluation proves the relevance of the proposed wavelet-based self-similar priors.

Supervised learning on graphs of spatio-temporal similarity in satellite image sequences

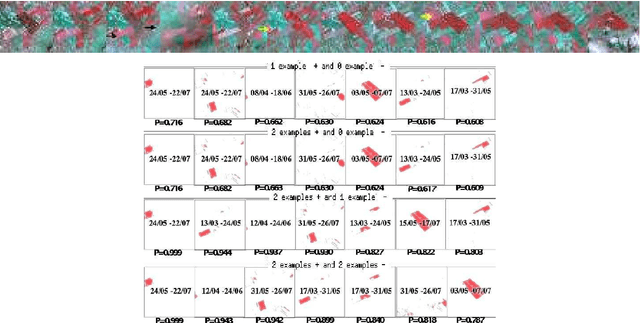
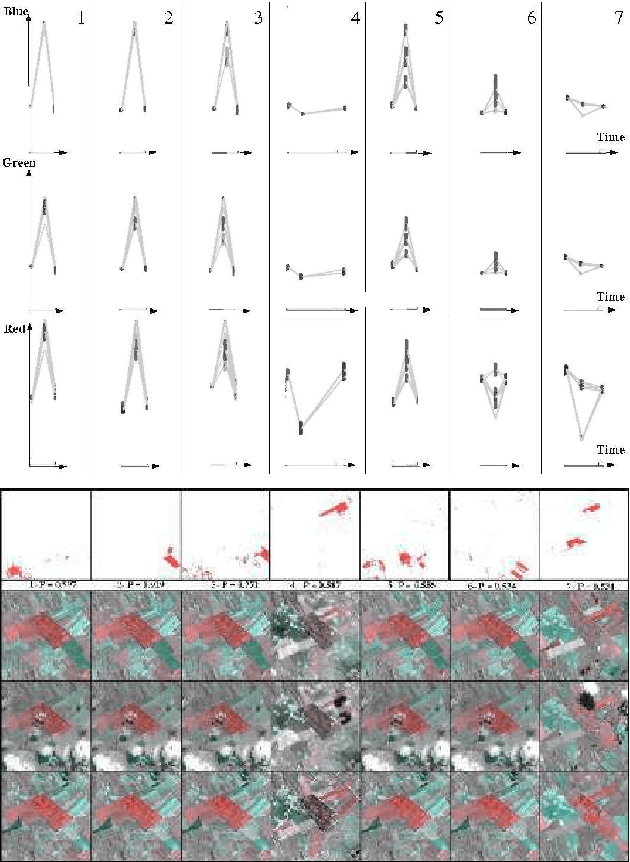
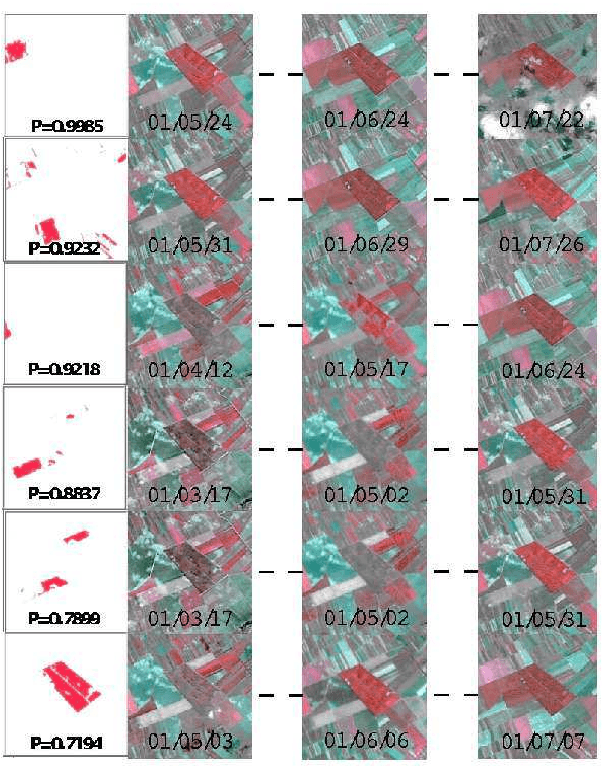
High resolution satellite image sequences are multidimensional signals composed of spatio-temporal patterns associated to numerous and various phenomena. Bayesian methods have been previously proposed in (Heas and Datcu, 2005) to code the information contained in satellite image sequences in a graph representation using Bayesian methods. Based on such a representation, this paper further presents a supervised learning methodology of semantics associated to spatio-temporal patterns occurring in satellite image sequences. It enables the recognition and the probabilistic retrieval of similar events. Indeed, graphs are attached to statistical models for spatio-temporal processes, which at their turn describe physical changes in the observed scene. Therefore, we adjust a parametric model evaluating similarity types between graph patterns in order to represent user-specific semantics attached to spatio-temporal phenomena. The learning step is performed by the incremental definition of similarity types via user-provided spatio-temporal pattern examples attached to positive or/and negative semantics. From these examples, probabilities are inferred using a Bayesian network and a Dirichlet model. This enables to links user interest to a specific similarity model between graph patterns. According to the current state of learning, semantic posterior probabilities are updated for all possible graph patterns so that similar spatio-temporal phenomena can be recognized and retrieved from the image sequence. Few experiments performed on a multi-spectral SPOT image sequence illustrate the proposed spatio-temporal recognition method.