A registration error estimation framework for correlative imaging

Correlative imaging workflows are now widely used in bioimaging and aims to image the same sample using at least two different and complementary imaging modalities. Part of the workflow relies on finding the transformation linking a source image to a target image. We are specifically interested in the estimation of registration error in point-based registration. We propose an application of multivariate linear regression to solve the registration problem allowing us to propose a framework for the estimation of the associated error in the case of rigid and affine transformations and with anisotropic noise. These developments can be used as a decision-support tool for the biologist to analyze multimodal correlative images and are available under Ec-CLEM, an open-source plugin under ICY.

Self-similar prior and wavelet bases for hidden incompressible turbulent motion

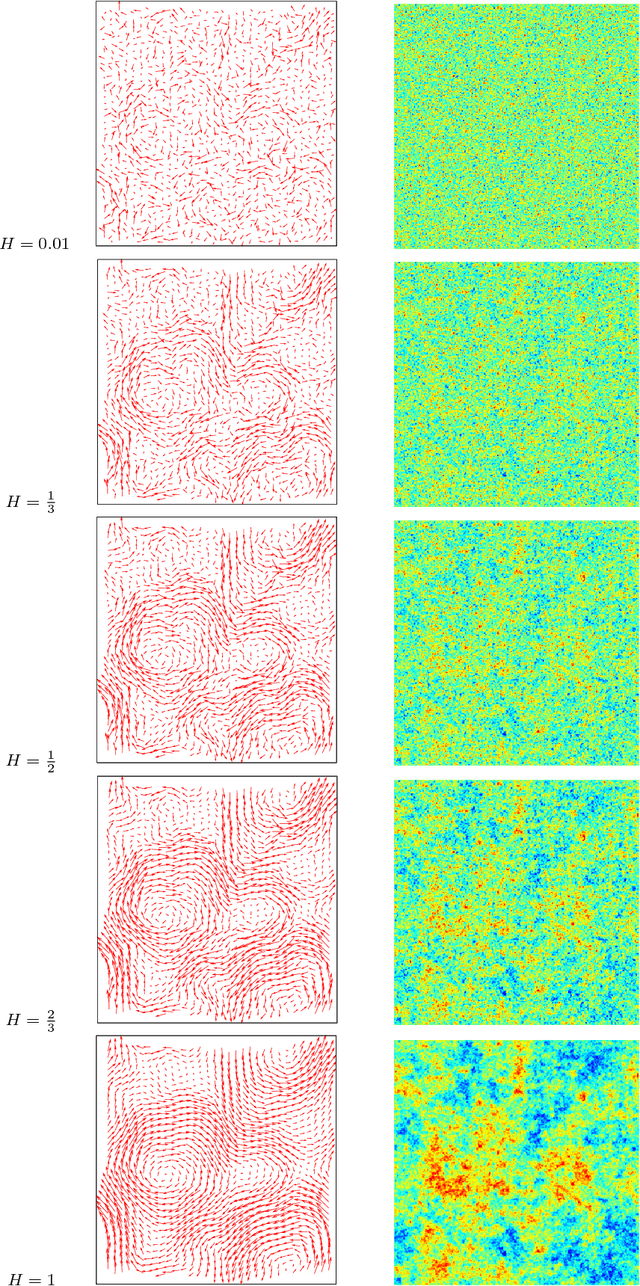
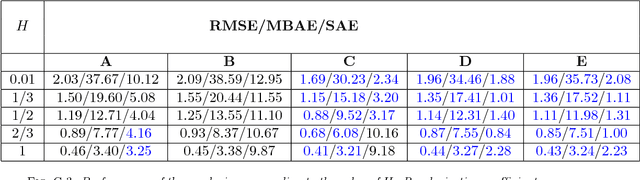
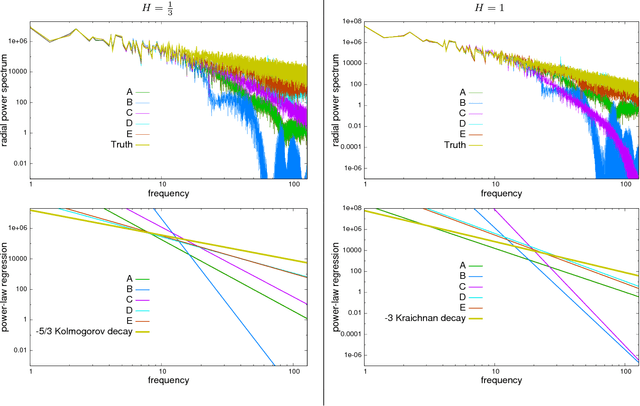
This work is concerned with the ill-posed inverse problem of estimating turbulent flows from the observation of an image sequence. From a Bayesian perspective, a divergence-free isotropic fractional Brownian motion (fBm) is chosen as a prior model for instantaneous turbulent velocity fields. This self-similar prior characterizes accurately second-order statistics of velocity fields in incompressible isotropic turbulence. Nevertheless, the associated maximum a posteriori involves a fractional Laplacian operator which is delicate to implement in practice. To deal with this issue, we propose to decompose the divergent-free fBm on well-chosen wavelet bases. As a first alternative, we propose to design wavelets as whitening filters. We show that these filters are fractional Laplacian wavelets composed with the Leray projector. As a second alternative, we use a divergence-free wavelet basis, which takes implicitly into account the incompressibility constraint arising from physics. Although the latter decomposition involves correlated wavelet coefficients, we are able to handle this dependence in practice. Based on these two wavelet decompositions, we finally provide effective and efficient algorithms to approach the maximum a posteriori. An intensive numerical evaluation proves the relevance of the proposed wavelet-based self-similar priors.