Uncertainty of Atmospheric Motion Vectors by Sampling Tempered Posterior Distributions
Paper and Code
Jul 08, 2022
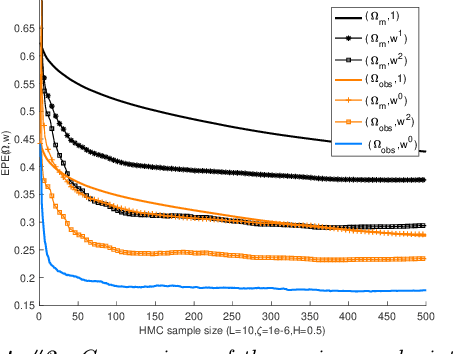
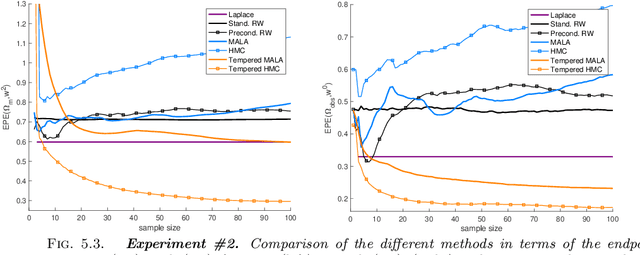
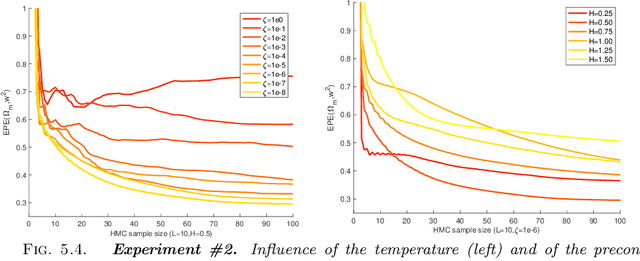
Atmospheric motion vectors (AMVs) extracted from satellite imagery are the only wind observations with good global coverage. They are important features for feeding numerical weather prediction (NWP) models. Several Bayesian models have been proposed to estimate AMVs. Although critical for correct assimilation into NWP models, very few methods provide a thorough characterization of the estimation errors. The difficulty of estimating errors stems from the specificity of the posterior distribution, which is both very high dimensional, and highly ill-conditioned due to a singular likelihood, which becomes critical in particular in the case of missing data (unobserved pixels). This work studies the evaluation of the expected error of AMVs using gradient-based Markov Chain Monte Carlo (MCMC) algorithms. Our main contribution is to propose a tempering strategy, which amounts to sampling a local approximation of the joint posterior distribution of AMVs and image variables in the neighborhood of a point estimate. In addition, we provide efficient preconditioning with the covariance related to the prior family itself (fractional Brownian motion), with possibly different hyper-parameters. From a theoretical point of view, we show that under regularity assumptions, the family of tempered posterior distributions converges in distribution as temperature decreases to an {optimal} Gaussian approximation at a point estimate given by the Maximum A Posteriori (MAP) log-density. From an empirical perspective, we evaluate the proposed approach based on some quantitative Bayesian evaluation criteria. Our numerical simulations performed on synthetic and real meteorological data reveal a significant gain in terms of accuracy of the AMV point estimates and of their associated expected error estimates, but also a substantial acceleration in the convergence speed of the MCMC algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge