Asymptotic Stability in Reservoir Computing

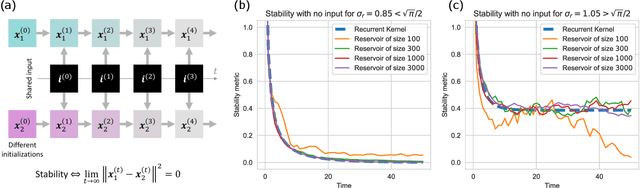
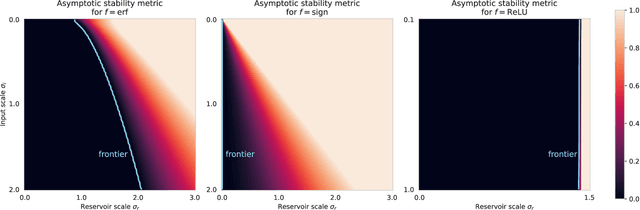
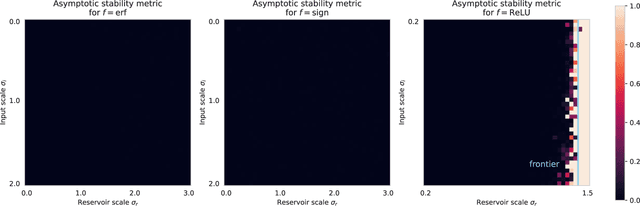
Reservoir Computing is a class of Recurrent Neural Networks with internal weights fixed at random. Stability relates to the sensitivity of the network state to perturbations. It is an important property in Reservoir Computing as it directly impacts performance. In practice, it is desirable to stay in a stable regime, where the effect of perturbations does not explode exponentially, but also close to the chaotic frontier where reservoir dynamics are rich. Open questions remain today regarding input regularization and discontinuous activation functions. In this work, we use the recurrent kernel limit to draw new insights on stability in reservoir computing. This limit corresponds to large reservoir sizes, and it already becomes relevant for reservoirs with a few hundred neurons. We obtain a quantitative characterization of the frontier between stability and chaos, which can greatly benefit hyperparameter tuning. In a broader sense, our results contribute to understanding the complex dynamics of Recurrent Neural Networks.

Reservoir Computing meets Recurrent Kernels and Structured Transforms

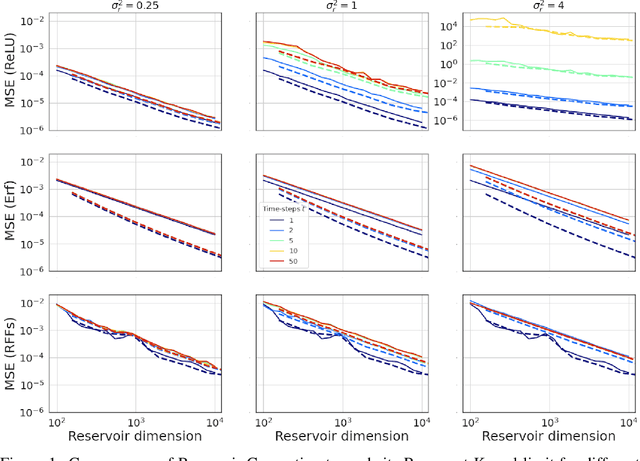
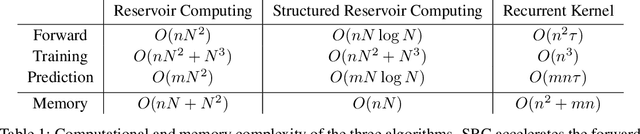
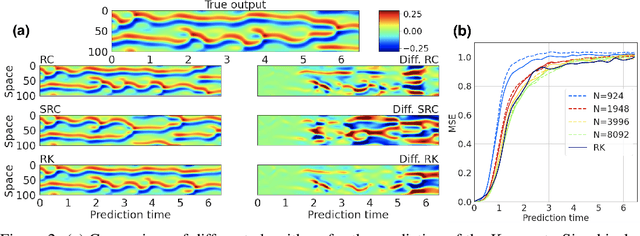
Reservoir Computing is a class of simple yet efficient Recurrent Neural Networks where internal weights are fixed at random and only a linear output layer is trained. In the large size limit, such random neural networks have a deep connection with kernel methods. Our contributions are threefold: a) We rigorously establish the recurrent kernel limit of Reservoir Computing and prove its convergence. b) We test our models on chaotic time series prediction, a classic but challenging benchmark in Reservoir Computing, and show how the Recurrent Kernel is competitive and computationally efficient when the number of data points remains moderate. c) When the number of samples is too large, we leverage the success of structured Random Features for kernel approximation by introducing Structured Reservoir Computing. The two proposed methods, Recurrent Kernel and Structured Reservoir Computing, turn out to be much faster and more memory-efficient than conventional Reservoir Computing.