G-computation for increasing performances of clinical trials with individual randomization and binary response

In a clinical trial, the random allocation aims to balance prognostic factors between arms, preventing true confounders. However, residual differences due to chance may introduce near-confounders. Adjusting on prognostic factors is therefore recommended, especially because the related increase of the power. In this paper, we hypothesized that G-computation associated with machine learning could be a suitable method for randomized clinical trials even with small sample sizes. It allows for flexible estimation of the outcome model, even when the covariates' relationships with outcomes are complex. Through simulations, penalized regressions (Lasso, Elasticnet) and algorithm-based methods (neural network, support vector machine, super learner) were compared. Penalized regressions reduced variance but may introduce a slight increase in bias. The associated reductions in sample size ranged from 17\% to 54\%. In contrast, algorithm-based methods, while effective for larger and more complex data structures, underestimated the standard deviation, especially with small sample sizes. In conclusion, G-computation with penalized models, particularly Elasticnet with splines when appropriate, represents a relevant approach for increasing the power of RCTs and accounting for potential near-confounders.

Wasserstein Random Forests and Applications in Heterogeneous Treatment Effects

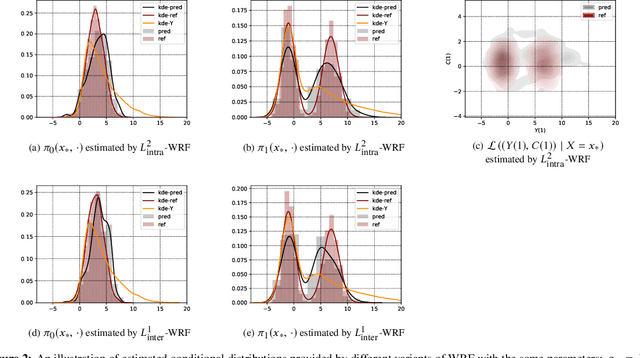
We present new insights into causal inference in the context of Heterogeneous Treatment Effects by proposing natural variants of Random Forests to estimate the key conditional distributions. To achieve this, we recast Breiman's original splitting criterion in terms of Wasserstein distances between empirical measures. This reformulation indicates that Random Forests are well adapted to estimate conditional distributions and provides a natural extension of the algorithm to multivariate outputs. Following the philosophy of Breiman's construction, we propose some variants of the splitting rule that are well-suited to the conditional distribution estimation problem. Some preliminary theoretical connections are established along with various numerical experiments, which show how our approach may help to conduct more transparent causal inference in complex situations.