Embedding and learning with signatures
Paper and Code
Nov 29, 2019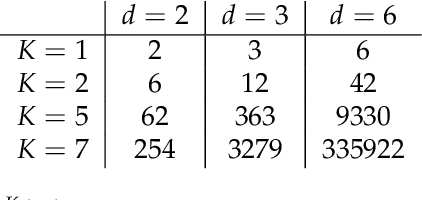
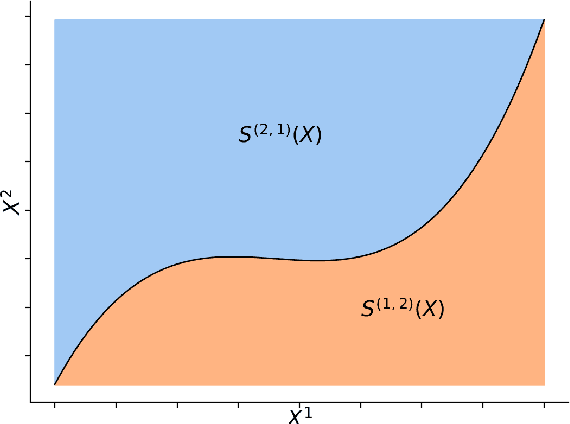
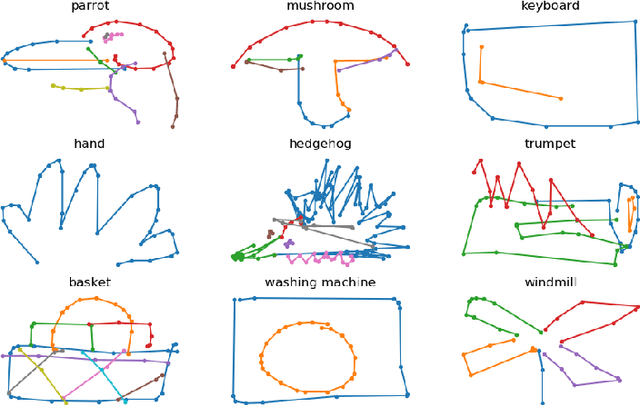
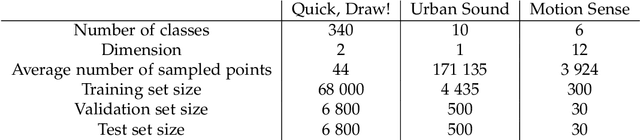
Sequential and temporal data arise in many fields of research, such as quantitative finance, medicine, or computer vision. The present article is concerned with a novel approach for sequential learning, called the signature method, and rooted in rough path theory. Its basic principle is to represent multidimensional paths by a graded feature set of their iterated integrals, called the signature. This approach relies critically on an embedding principle, which consists in representing discretely sampled data as paths, i.e., functions from $[0,1]$ to $R^d$. After a survey of machine learning methodologies for signatures, we investigate the influence of embeddings on prediction accuracy with an in-depth study of three recent and challenging datasets. We show that a specific embedding, called lead-lag, is systematically better, whatever the dataset or algorithm used. Moreover, we emphasize through an empirical study that computing signatures over the whole path domain does not lead to a loss of local information. We conclude that, with a good embedding, the signature combined with a simple algorithm achieves results competitive with state-of-the-art, domain-specific approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge